题目内容
观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
…
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
根据上述各式反映的规律填空,使式子称为“数字对称等式”:
(1)52× = ×25;
(2) ×396=693× .
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
…
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
根据上述各式反映的规律填空,使式子称为“数字对称等式”:
(1)52×
(2)
考点:规律型:数字的变化类
专题:规律型
分析:(1)根据排列规律,个位与十位数字分别放到百位与个位上,它们的和作为十位数字,写出即可;
(2)观察排列规律,百位与个位数字分别作为两位数的个位和十位上的数字即可.
(2)观察排列规律,百位与个位数字分别作为两位数的个位和十位上的数字即可.
解答:解:(1)52×275=572×25;
(2)63×396=693×36.
故答案为:275,572;63,36.
(2)63×396=693×36.
故答案为:275,572;63,36.
点评:本题是对数字变化规律的考查,观察等式得到两位数与三位数的数字之间的变化规律是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
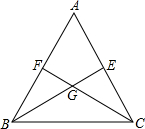 如图,△ABC中,∠ABC和∠ACB的平分线BE,CF相交于点G.求证:
如图,△ABC中,∠ABC和∠ACB的平分线BE,CF相交于点G.求证:
 如图,AE=AF,点B、D分别在AE、AF上,四边形ABCD是菱形,连接EC、FC
如图,AE=AF,点B、D分别在AE、AF上,四边形ABCD是菱形,连接EC、FC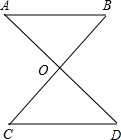 (1)计算:(π-3)0+
(1)计算:(π-3)0+