题目内容
如图,一块直径为10cm(即AB=10cm)的量角器,若将量角器与∠MPN按如图1叠放(A与P重合,AB与PM重合),并已知点B、C、A处的读数分别为0°、40°、180°.
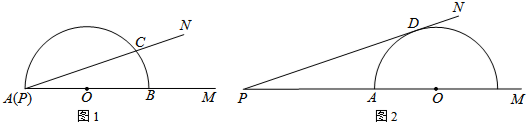
(1)∠MPN的度数是 .
(2)求线段PC的长.
(3)在图1的状态下,∠MPN不动,将量角器沿着射线PM向右平移(如图2),问平移多少厘米后量角器与PN相切于点D?切点D处的读数是多少?(可用计算器,结果精确到0.1cm)

(1)∠MPN的度数是
(2)求线段PC的长.
(3)在图1的状态下,∠MPN不动,将量角器沿着射线PM向右平移(如图2),问平移多少厘米后量角器与PN相切于点D?切点D处的读数是多少?(可用计算器,结果精确到0.1cm)
考点:切线的性质,圆周角定理,解直角三角形
专题:
分析:(1)如图1,连接OC,利用“在同圆中,同弧所对的圆周角是所对的圆心角的一半”填空;
(2)如图1,连接BC.构建直角△ACB,通过解直角三角形来求PC的长度;
(3)如图2,连接OD.利用切线的性质判定△PDO是直角三角形,通过解该直角三角形来求PA的长度;由三角形外角定理来求点D所表示的读数.
(2)如图1,连接BC.构建直角△ACB,通过解直角三角形来求PC的长度;
(3)如图2,连接OD.利用切线的性质判定△PDO是直角三角形,通过解该直角三角形来求PA的长度;由三角形外角定理来求点D所表示的读数.
解答: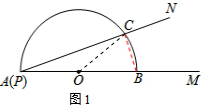 解:(1)如图1,
解:(1)如图1,
∵点B、C、A处的读数分别为0°、40°、180°,
∴∠COB=40°,
∴∠MPN=
∠COB=20°.
故填:20°;
(2)如图1,连接BC.
∵AB是直径,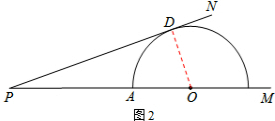
∴∠ACB=90°,
∴cos20°=
.
即PC=AB•cos20°=10×cos20°≈10×0.94=9.4(cm);
(3)如图2,连接OD.
∵PD与半圆切于点D,
∵∠PDO=90°.
则在Rt△PDO中,由于∠P=20°,OD=5cm,
∴sin20°=
,OP=
≈14.6.
∴PA=14.6-5=9.6(cm).
又∵∠DOM=90°+20°=110°,
∴切点D处的读数为110°.
 解:(1)如图1,
解:(1)如图1,∵点B、C、A处的读数分别为0°、40°、180°,
∴∠COB=40°,
∴∠MPN=
| 1 |
| 2 |
故填:20°;
(2)如图1,连接BC.
∵AB是直径,

∴∠ACB=90°,
∴cos20°=
| PC |
| AB |
即PC=AB•cos20°=10×cos20°≈10×0.94=9.4(cm);
(3)如图2,连接OD.
∵PD与半圆切于点D,
∵∠PDO=90°.
则在Rt△PDO中,由于∠P=20°,OD=5cm,
∴sin20°=
| 5 |
| OP |
| 5 |
| sin20° |
∴PA=14.6-5=9.6(cm).
又∵∠DOM=90°+20°=110°,
∴切点D处的读数为110°.
点评:本题考查了切线的性质,圆周角定理和解直角三角形.解题时,需要熟悉量角器的使用方法.

练习册系列答案
相关题目
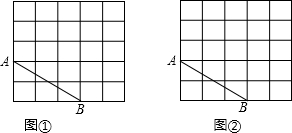 如图,在每个小正方形的边长均为1的方格纸中有一条线段AB,线段AB的两个端点均在小正方形的顶点上,请在图①、图②中各画一个三角形,它们的顶点均在小正方形的顶点上,且满足以下要求:
如图,在每个小正方形的边长均为1的方格纸中有一条线段AB,线段AB的两个端点均在小正方形的顶点上,请在图①、图②中各画一个三角形,它们的顶点均在小正方形的顶点上,且满足以下要求: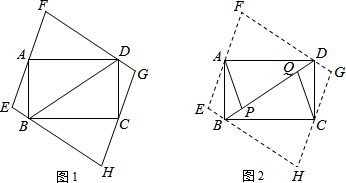

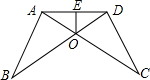 如图,AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE
如图,AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE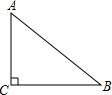 已知在Rt△ABC中,∠C=90°,AB=25,AC=20,求△ABC的周长.
已知在Rt△ABC中,∠C=90°,AB=25,AC=20,求△ABC的周长.