题目内容
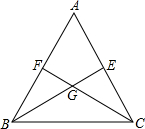 如图,△ABC中,∠ABC和∠ACB的平分线BE,CF相交于点G.求证:
如图,△ABC中,∠ABC和∠ACB的平分线BE,CF相交于点G.求证:(1)∠BGC=180°-
| 1 |
| 2 |
(2)∠BGC=90°+
| 1 |
| 2 |
考点:三角形内角和定理,三角形的外角性质
专题:证明题
分析:(1)根据角平分线的定义可得∠GBC=
∠ABC,∠GCB=
∠ACB,然后利用三角形的内角和定理列式整理即可;
(2)根据三角形的内角和定理可得∠ABC+∠ACB=180°-∠A,然后代入整理即可得证.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据三角形的内角和定理可得∠ABC+∠ACB=180°-∠A,然后代入整理即可得证.
解答:证明:(1)∵∠ABC和∠ACB的平分线BE,CF相交于点G,
∴∠GBC=
∠ABC,∠GCB=
∠ACB,
∴∠GBC+∠GCB=
(∠ABC+∠ACB),
在△BCG中,∠BGC=180°-(∠GBC+∠GCB)=180°-
(∠ABC+∠ACB);
即:∠BGC=180°-
(∠ABC+∠ACB);
(2)在△ABC中,∠ABC+∠ACB=180°-∠A,
所以,∠BGC=180°-
(∠ABC+∠ACB)=180°-
(180°-∠A)=90°+
∠A,
即:∠BGC=90°+
∠A.
∴∠GBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GBC+∠GCB=
| 1 |
| 2 |
在△BCG中,∠BGC=180°-(∠GBC+∠GCB)=180°-
| 1 |
| 2 |
即:∠BGC=180°-
| 1 |
| 2 |
(2)在△ABC中,∠ABC+∠ACB=180°-∠A,
所以,∠BGC=180°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即:∠BGC=90°+
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,是基础题,熟记定理并准确识图是解题的关键,要注意整体思想的利用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
方程(
)x+(
)x=4的解x等于( )
2+
|
2-
|
| A、2 | B、-2 | C、2或-2 | D、无解 |
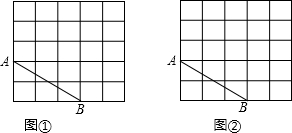 如图,在每个小正方形的边长均为1的方格纸中有一条线段AB,线段AB的两个端点均在小正方形的顶点上,请在图①、图②中各画一个三角形,它们的顶点均在小正方形的顶点上,且满足以下要求:
如图,在每个小正方形的边长均为1的方格纸中有一条线段AB,线段AB的两个端点均在小正方形的顶点上,请在图①、图②中各画一个三角形,它们的顶点均在小正方形的顶点上,且满足以下要求: 某校各选拔了5名同学参加学校举行的“安全知识”比赛活动,比赛结果如图.
某校各选拔了5名同学参加学校举行的“安全知识”比赛活动,比赛结果如图.