题目内容
矩形ABCD的边AB=10,BC=6,E是BC上一点,将矩形沿AE折叠,点B恰好落在CD边上的F点,求BE的长.
考点:翻折变换(折叠问题)
专题:
分析:作出图形,根据翻折的性质可得AF=AB,BE=EF,利用勾股定理列式求出DF,再求出FC,设BE=x,表示出CE=6-x,在Rt△CEF中,利用勾股定理列出方程求解即可.
解答: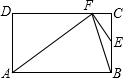 解:如图,∵BC=6,
解:如图,∵BC=6,
∴AD=BC=6,CD=AB=10,
由翻折的性质得AF=AB=10,BE=EF,
在Rt△ADF中,DF=
=
=8,
∴FC=CD-DF=10-8=2,
设BE=x,则CE=6-x,
在Rt△CEF中,FC2+CE2=EF2,
即22+(6-x)2=x2,
解得x=
,
即BE=
.
 解:如图,∵BC=6,
解:如图,∵BC=6,∴AD=BC=6,CD=AB=10,
由翻折的性质得AF=AB=10,BE=EF,
在Rt△ADF中,DF=
| AF2-AD2 |
| 102-62 |
∴FC=CD-DF=10-8=2,
设BE=x,则CE=6-x,
在Rt△CEF中,FC2+CE2=EF2,
即22+(6-x)2=x2,
解得x=
| 10 |
| 3 |
即BE=
| 10 |
| 3 |
点评:本题考查了翻折变换的性质,勾股定理,熟记性质并利用勾股定理列出方程是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
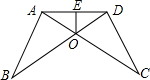 如图,AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE
如图,AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE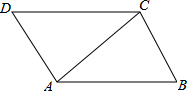 (1)已知:如图,∠BAC=∠DCA,∠BCA=∠DAC,求证:△ABC≌△CDA.
(1)已知:如图,∠BAC=∠DCA,∠BCA=∠DAC,求证:△ABC≌△CDA. 如图,已知AB=CB,DB=EB,∠ABD=∠CBE,求证:AD=EC.
如图,已知AB=CB,DB=EB,∠ABD=∠CBE,求证:AD=EC.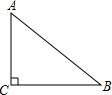 已知在Rt△ABC中,∠C=90°,AB=25,AC=20,求△ABC的周长.
已知在Rt△ABC中,∠C=90°,AB=25,AC=20,求△ABC的周长.