题目内容
 (1)计算:(π-3)0+
(1)计算:(π-3)0+| 12 |
| 1 |
| 2 |
| 3 |
(2)作一次函数y=x-1的图象;
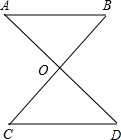
(3)已知:如图,AD,BC相交于点O,OA=OD,AB∥CD,求证:AB=CD.
考点:全等三角形的判定与性质,实数的运算,零指数幂,负整数指数幂,一次函数的图象,特殊角的三角函数值
专题:计算题
分析:(1)原式第一项利用零指数幂法则计算,第二项化为最简二次根式,第三项利用特殊角的三角函数值 计算,第四项利用负指数幂法则计算,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)分别令x与y为0求出y与x的值,确定出两点坐标,做出一次函数y=x-1的图象即可;
(3)由AB与CD平行,利用两直线平行内错角相等得到两对角相等,再由OA=OD,利用AAS得到三角形AOB与三角形COD全等,利用全等三角形的对应边相等即可得证.
(2)分别令x与y为0求出y与x的值,确定出两点坐标,做出一次函数y=x-1的图象即可;
(3)由AB与CD平行,利用两直线平行内错角相等得到两对角相等,再由OA=OD,利用AAS得到三角形AOB与三角形COD全等,利用全等三角形的对应边相等即可得证.
解答:解:(1)原式=1+2
-2×
+2+2-
=5;
(2)令x=0,得到y=1;令y=0,得到x=1,
∴一次函数图象上坐标为(0,1),(1,0),

(3)证明:∵AB∥CD,
∴∠A=∠D,∠B=∠D,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS),
∴AB=CD.
| 3 |
| ||
| 2 |
| 3 |
(2)令x=0,得到y=1;令y=0,得到x=1,
∴一次函数图象上坐标为(0,1),(1,0),

(3)证明:∵AB∥CD,
∴∠A=∠D,∠B=∠D,
在△AOB和△DOC中,
|
∴△AOB≌△DOC(AAS),
∴AB=CD.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 某校各选拔了5名同学参加学校举行的“安全知识”比赛活动,比赛结果如图.
某校各选拔了5名同学参加学校举行的“安全知识”比赛活动,比赛结果如图.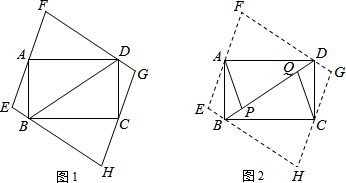
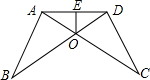 如图,AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE
如图,AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE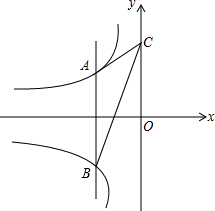 如图,动点A在双曲线y=-
如图,动点A在双曲线y=-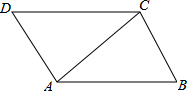 (1)已知:如图,∠BAC=∠DCA,∠BCA=∠DAC,求证:△ABC≌△CDA.
(1)已知:如图,∠BAC=∠DCA,∠BCA=∠DAC,求证:△ABC≌△CDA.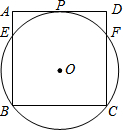 如图,正方形ABCD的边AD与⊙O相切于点P,E、F是正方形与圆的另两个交点.若BC=4,则
如图,正方形ABCD的边AD与⊙O相切于点P,E、F是正方形与圆的另两个交点.若BC=4,则