题目内容
17. 如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )
如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
分析 分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,由对称的性质得出PM=DM,OP=OC,∠COA=∠POA;PN=CN,OP=OD,∠DOB=∠POB,得出∠AOB=$\frac{1}{2}$∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
解答 解:分别作点P关于OA、OB的对称点C、D,连接CD,
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB=$\frac{1}{2}$∠COD,
∵△PMN周长的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°;
故选:B.
点评 本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质;熟练掌握轴对称的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
8.在平面直角坐标系中,已知点P的坐标是(6,8),则OP的长为( )
| A. | $\sqrt{7}$ | B. | 8 | C. | 9 | D. | 10 |
5.某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”,“诚实守信”四种类别,每位同学只能参评其中一类,评选后,把最终入选的20位校园“美德少年”分类统计,制作了如下统计表,后来发现,统计表中前两行的数据都是正确的,后两行的数据中有一个是错误的.
根据以上信息,解答下列问题:
(1)统计表中的a=4,b0.15;
(2)统计表后两行错误的数据是0.32,该数据的正确值是0.30;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.
| 类别 | 频数 | 频率 |
| 助人为乐美德少年 | a | 0.20 |
| 自强自立美德少年 | 3 | b |
| 孝老爱亲美德少年 | 7 | 0.35 |
| 诚实守信美德少年 | 6 | 0.32 |
(1)统计表中的a=4,b0.15;
(2)统计表后两行错误的数据是0.32,该数据的正确值是0.30;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.
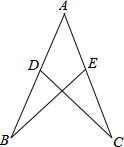 如图,点D在AB上,点E在AC上,AB=AC,AD=AE.求证:BE=CD.
如图,点D在AB上,点E在AC上,AB=AC,AD=AE.求证:BE=CD. 一只自由飞行的小鸟,将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在白色方格地面上的概率是$\frac{3}{4}$.
一只自由飞行的小鸟,将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在白色方格地面上的概率是$\frac{3}{4}$. 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.