题目内容
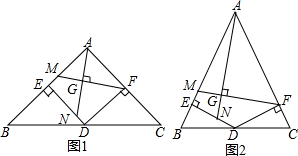
18.已知如图1、2,D是△ABC的BC边上的中点,DE⊥AB于E、DF⊥AC于F,且BE=CF,点M、N分别是AE、DE上的点,AN⊥FM于G(1)如图1,当∠BAC=90°时;
①求证:四边形AEDF是正方形;
②试问AN与FM之间的数量关系与四边形AEDF的两对角线的数量关系相同吗?请证明你的结论;
(2)如图2,当∠BAC≠90°,且AF:DF=2:1时,求AN:FM的值;
(3)根据(1)中②和(2)的结论或求解过程,在一般情况下(即除去条件:“∠BAC-90°,AF:DF=2:1”,其他条件不变),问AN与FM之间的数量关系有何规律?直接用文字说明或用等式表示(不证明).
分析 (1)①证明Rt△BED≌Rt△CFD,得到DE=DF,证明结论;
②根据已知和正方形的性质证明Rt△AEN≌Rt△FAM,得到答案;
(2)根据已知设AF=2k,DF=k,求出AD:EF,证明△FME∽△AND,求出AN:FM的值;
(3)根据(1)中②和(2)的结论,可以得到AN与FM之间的数量关系与四边形AEDF的两条对角线之间的关系.
解答 (1)①证明:∵∠BAC=90°,∠AED=∠AFD=90°,
∴四边形AEDF是矩形,
以上BD=DC,∠DEB=∠DFC=90°,BE=CF,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∴矩形AEDF是正方形.
②答:AN与FM之间的数量关系与四边形AEDF的两条对角线的数量关系相同;
理由:在正方形AEDF中,AF=AE,
又∵AN⊥FM于G,∠AMF=∠ANE,
∠AEN=∠MAF=90°,
∴Rt△AEN≌Rt△FAM(AAS),
∴AN=FM,
又∵正方形AEDF的对角线相等,
∴AN与FM之间的数量关系与四边形AEDF的两对角线的数量关系相同.
(2)连接AD、EF,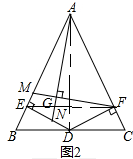
设AF=2k,DF=k,在Rt△ADF中,AD=$\sqrt{(2k)^{2}+{k}^{2}}$=$\sqrt{5}$k,
∵Rt△BED≌Rt△CFD(HL),
∴∠B=∠C,DE=DF,
∴AB=AC,AE=AF,
∴AD的垂直平分EF,则OF=$\frac{1}{2}$EF,DF⊥AC与F,
$\frac{1}{2}×\sqrt{5}k•OF$=2k×k×$\frac{1}{2}$,
∴PF=$\frac{2k}{\sqrt{5}}$,
∴EF=$\frac{4k}{\sqrt{5}}$,
又∵∠NEM=∠MGN=90°,
∠GME+∠ENG=∠DNG+∠ENG=180°,
∠EMF=∠DNA,∠AEO=∠NDA,
∴△FME∽△AND,
∴$\frac{AN}{FM}$=$\frac{AD}{EF}$=$\frac{5}{4}$;
(3)根据(1)中②和(2)的结论或求解过程可知,
∵∠NEM=∠MGN=90°,
∠GME+∠ENG=∠DNG+∠ENG=180°,
∠EMF=∠DNA,∠AEO=∠NDA,
∴△FME∽△AND,
∴$\frac{AN}{FM}$=$\frac{AD}{EF}$,
AN、FM与四边形AEDF的两条对角线对应成比例.
点评 本题考查的是相似三角形的判定和性质、全等三角形的判定和性质,灵活运用判定定理和性质定理是解题的关键,注意方程思想在解题中的运用.

| A. | b=-3 | B. | b=-2 | C. | b=-1 | D. | b=2 |
| A. | $\sqrt{7}$ | B. | 8 | C. | 9 | D. | 10 |
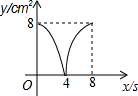
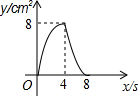
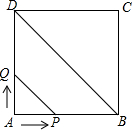 如图,正方形ABCD的边长为4cm,动点p,Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )
如图,正方形ABCD的边长为4cm,动点p,Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )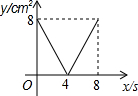
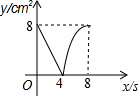
 如图,在△ABC中,∠A=30°,∠B=55°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的B′处
如图,在△ABC中,∠A=30°,∠B=55°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的B′处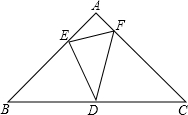 已知△ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,点D位于边BC的中点上,点E在AB上,点F在AC上,∠EDF=45°.
已知△ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,点D位于边BC的中点上,点E在AB上,点F在AC上,∠EDF=45°.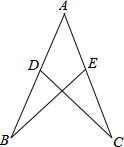 如图,点D在AB上,点E在AC上,AB=AC,AD=AE.求证:BE=CD.
如图,点D在AB上,点E在AC上,AB=AC,AD=AE.求证:BE=CD.