题目内容
7. 如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AC=6,求:(1)AB的长;
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AC=6,求:(1)AB的长;(2)矩形ABCD的面积.
分析 (1)根据OB=OC,∠ABC=90°,以及∠BOC=120°,可得出∠OBC=∠OCB=30°,进而得到AB=$\frac{1}{2}$AC=3;
(2)根据勾股定理即可得出BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=3$\sqrt{3}$,进而得出矩形ABCD的面积.
解答 解:(1)∵四边形ABCD是矩形,
∴OB=OC,∠ABC=90°,
又∵∠BOC=120°,
∴∠OBC=∠OCB=30°,
∴AB=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3;
(2)∵AB2+BC2=AC2,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=3$\sqrt{3}$,
∴矩形ABCD的面积=AB×BC=3×3$\sqrt{3}$=9$\sqrt{3}$.
点评 本题主要考查了矩形的性质以及勾股定理的运用,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
相关题目
17.已知一个三角形的两边长分别是2和6,第三边为偶数,则此三角形的周长是( )
| A. | 13 | B. | 14 | C. | 15 | D. | 13或15 |
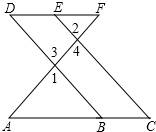 完成下面的证明.如图,E点位DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.
完成下面的证明.如图,E点位DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.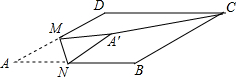 如图,在平行四边形ABCD中,∠BCD=30°,BC=6,CD=$6\sqrt{3}$,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线
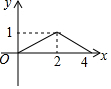
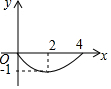
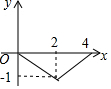
如图,在平行四边形ABCD中,∠BCD=30°,BC=6,CD=$6\sqrt{3}$,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线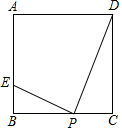 如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )
如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )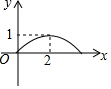
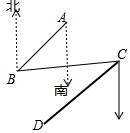 如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.
如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.