题目内容
16.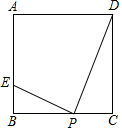 如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )
如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )| A. | 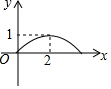 | B. | 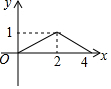 | C. | 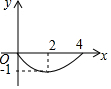 | D. | 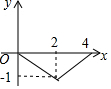 |
分析 由题意知:PE⊥DP,即:∠DPC+∠EPB=90°,∠BPE+∠PEB=180°-∠B=90°,所以∠DPC=∠BEP,又∠B=∠C,即:△EBP∽△PCD,由相似三角形的性质可得:$\frac{BE}{PC}$=$\frac{BP}{CD}$,又BP=x,PC=BC-BP=4-x,CD=4,将其代入该式求出CP的值即可.
解答 解:∵四边形ABCD是正方形,
∴∠B=∠C=90°
∵PE⊥DP,
∴∠DPC+∠EPB=90°,∠BPE+∠PEB=180°-∠B=90°
∴∠DPC=∠BEP,又∠B=∠CBAP=∠QPC
∴△EBP∽△PCD,
∴$\frac{BE}{PC}$=$\frac{BP}{CD}$,又BP=x,PC=BC-BP=4-x,CD=4,BE=y,
即$\frac{y}{4-x}$=$\frac{x}{4}$,
∴y=-$\frac{1}{4}$x2+x(0<x<4),
故选A.
点评 本题考查了正方形的性质和二次函数的应用,关键在于理解题意运用三角形的相似性质求出y与x之间的函数关系,求最大值时,运用到“配方法”.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.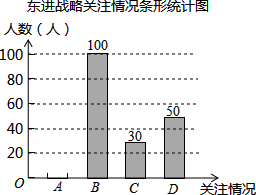 为了解汕头市民对创建文明城市的关注情况,某校数学兴趣小组随机采访部分汕头市民,对采访情况制作了统计图表的一部分如下:
为了解汕头市民对创建文明城市的关注情况,某校数学兴趣小组随机采访部分汕头市民,对采访情况制作了统计图表的一部分如下:
(1)根据上述统计图可得此次采访的人数为200人,M=20,N=0.15;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名汕头市民中,高度关注创建文明城市的汕头市民约有1500人.
 为了解汕头市民对创建文明城市的关注情况,某校数学兴趣小组随机采访部分汕头市民,对采访情况制作了统计图表的一部分如下:
为了解汕头市民对创建文明城市的关注情况,某校数学兴趣小组随机采访部分汕头市民,对采访情况制作了统计图表的一部分如下:| 关注情况 | 频数 | 频率 |
| A.高度关注 | M | 0.1 |
| B.一般关注 | 100 | 0.5 |
| C.不关注 | 30 | N |
| D.不知道 | 50 | 0.25 |
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名汕头市民中,高度关注创建文明城市的汕头市民约有1500人.
5.下列各式中不能用公式法分解因式的是( )
| A. | x2-6x+9 | B. | -x2+y2 | C. | x2+2x+4 | D. | -x2+2xy-y2 |
6.方程$\frac{3}{x-2}$+$\frac{1}{2-x}$=1的解为( )
| A. | -1 | B. | 1 | C. | 4 | D. | 5 |
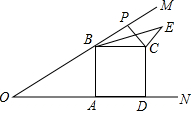 如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为2$\sqrt{3}$+2.
如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为2$\sqrt{3}$+2. 如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AC=6,求:(1)AB的长;
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AC=6,求:(1)AB的长;
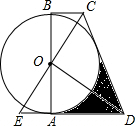 如图,AB为⊙O的直径,BC、AD是⊙O的切线,切点分别为B、A,过点O作EC⊥OD,EC交BC于点C,交AD于点E.
如图,AB为⊙O的直径,BC、AD是⊙O的切线,切点分别为B、A,过点O作EC⊥OD,EC交BC于点C,交AD于点E.