题目内容
13.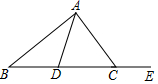 已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角.
已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角.(1)读下列语句,尺规作图,保留作图痕迹.
①作∠ACE的角平分线,交BA延长线于点F;
②过点D作DH∥AC,交AB于点H,连接CH.
(2)依据以上条件,解答下列问题.
①与△AHD面积相等的三角形是△BDH,△CDH;
②若∠B=40°,∠F=30°,求∠BAC的度数.
分析 (1)根据角平分线以及平行线的定义进行作图即可;
(2)①AC∥DH,可得△CDH与△AHD面积相等,再根据D是BC的中点,AC∥DH,可得△BDH与△AHD面积相等;
②根据BAC是△AFC的外角,可得∠BAC=∠ACF+∠F,根据∠FCE是△BFC的外角,可得∠FCE=∠B+∠F,再根据CF是∠ACE的角平分线,即可得出∠FCE=∠ACF,最后根据∠BAC=∠ACF+∠F=∠FCE+∠F=∠B+∠F+∠F进行计算即可.
解答 解:(1)如图所示,
(2)①∵AC∥DH,
∴△CDH与△AHD面积相等,
∵D是BC的中点,AC∥DH,
∴H是AB的中点,
∴△BDH与△AHD面积相等,
故答案为:△BDH,△CDH;
②∵∠BAC是△AFC的外角,
∴∠BAC=∠ACF+∠F,
∵∠FCE是△BFC的外角,
∴∠FCE=∠B+∠F,
∵CF是∠ACE的角平分线,
∴∠FCE=∠ACF,
∴∠BAC=∠ACF+∠F=∠FCE+∠F=∠B+∠F+∠F=40°+30°+30°=100°.
点评 本题主要考查了复杂作图,角平分线以及平行线的定义,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3.下列结论错误的是( )
| A. | 平行四边形既是中心对称又是轴对称图形 | |
| B. | 矩形的四个角相等 | |
| C. | 正方形的对角线互相垂直平分且相等 | |
| D. | 菱形的四条边相等 |
4.下列各数中,相反数为4的是( )
| A. | 4 | B. | -4 | C. | 0.4 | D. | 0.25 |
1.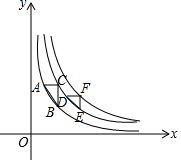 如图,△ABC和△DEF的各顶点分别在双曲线y=$\frac{1}{x}$,y=$\frac{2}{x}$,y=$\frac{3}{x}$在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC-S△DEF=( )
如图,△ABC和△DEF的各顶点分别在双曲线y=$\frac{1}{x}$,y=$\frac{2}{x}$,y=$\frac{3}{x}$在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC-S△DEF=( )
 如图,△ABC和△DEF的各顶点分别在双曲线y=$\frac{1}{x}$,y=$\frac{2}{x}$,y=$\frac{3}{x}$在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC-S△DEF=( )
如图,△ABC和△DEF的各顶点分别在双曲线y=$\frac{1}{x}$,y=$\frac{2}{x}$,y=$\frac{3}{x}$在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC-S△DEF=( )| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{12}$ |
5.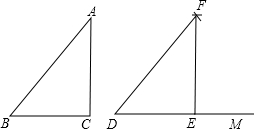 小明用如图所示的方法画出了与△ABC全等的△DEF,他的具体画法是:①画射线DM,在射线DM上截取DE=BC;②以点D为圆心,BA长为半径画弧,以点E为圆心,CA长为半径画弧,画弧相交于点F;③联结FD,FE;这样△DEF就是所要画的三角形,小明这样画图的依据是全等三角形判定方法中的( )
小明用如图所示的方法画出了与△ABC全等的△DEF,他的具体画法是:①画射线DM,在射线DM上截取DE=BC;②以点D为圆心,BA长为半径画弧,以点E为圆心,CA长为半径画弧,画弧相交于点F;③联结FD,FE;这样△DEF就是所要画的三角形,小明这样画图的依据是全等三角形判定方法中的( )
 小明用如图所示的方法画出了与△ABC全等的△DEF,他的具体画法是:①画射线DM,在射线DM上截取DE=BC;②以点D为圆心,BA长为半径画弧,以点E为圆心,CA长为半径画弧,画弧相交于点F;③联结FD,FE;这样△DEF就是所要画的三角形,小明这样画图的依据是全等三角形判定方法中的( )
小明用如图所示的方法画出了与△ABC全等的△DEF,他的具体画法是:①画射线DM,在射线DM上截取DE=BC;②以点D为圆心,BA长为半径画弧,以点E为圆心,CA长为半径画弧,画弧相交于点F;③联结FD,FE;这样△DEF就是所要画的三角形,小明这样画图的依据是全等三角形判定方法中的( )| A. | 边角边 | B. | 角边角 | C. | 角角边 | D. | 边边边 |
2.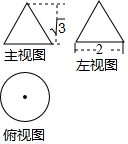 已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )
已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )
 已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )
已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )| A. | 2π | B. | 4π | C. | $\sqrt{3}$π | D. | 2$\sqrt{3}$π |
3. 如图,将△ABC绕点C(0,1)旋转180°得到△DEC.若点A的坐标为(3,-1),则点D的坐标为( )
如图,将△ABC绕点C(0,1)旋转180°得到△DEC.若点A的坐标为(3,-1),则点D的坐标为( )
 如图,将△ABC绕点C(0,1)旋转180°得到△DEC.若点A的坐标为(3,-1),则点D的坐标为( )
如图,将△ABC绕点C(0,1)旋转180°得到△DEC.若点A的坐标为(3,-1),则点D的坐标为( )| A. | (-3,1) | B. | (-2,2) | C. | (-3,3) | D. | (-3,2) |
 如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D. 如图,AB∥CD,AC∥BE,∠BAC=70°,∠CDE=35°,则∠BED=145°.
如图,AB∥CD,AC∥BE,∠BAC=70°,∠CDE=35°,则∠BED=145°.