题目内容
19.我市正大力倡导”垃圾分类“,2015年第一季度某企业按A类垃圾处理费25元/吨、B类垃圾处理费16元/吨的收费标准,共支付垃圾处理费520元.从2015年4月起,收费标准上调为:A类垃圾处理费100元/吨,B类垃圾处理费30元/吨.若该企业2015年第二季度需要处理的A类,B类垃圾的数量与第一季度相同,就要多支付垃圾处理费880元.(1)该企业第一季度处理的两类垃圾各多少吨?
(2)该企业计划第二季度将上述两种垃圾处理总量减少到24吨,且B类垃圾处理量不超过A类垃圾处理量的3倍,该企业第二季度最少需要支付这两种垃圾处理费共多少元?
分析 (1)该企业第一季度处理的A类垃圾x吨,B类垃圾y吨,根据等量关系式:A垃圾处理费25元/吨×A垃圾吨数+B处理费16元/吨×B垃圾吨数=总费用,列方程.
(2)设该企业2015年处理的A类垃圾a吨,根据B类垃圾处理量不超过A类垃圾处理量的3倍,列不等式求解.
解答 解:(1)该企业第一季度处理的A类垃圾x吨,B类垃圾y吨,根
由题意得,$\left\{\begin{array}{l}{25x+16y=520}\\{100x+30y=880+520}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=20}\end{array}\right.$,
答:该企业第一季度处理的A类垃圾8吨,B类垃圾20吨;
(2)设该企业2015年处理的A类垃圾a吨,
由题意得,24-a≤3a,
解得:a≥6,
则总费用为:100a+30(24-a)=720+70a,
当a为6时,有最小值:1140(元).
答:企业第二季度最少需要支付这两种垃圾处理费共1140元.
点评 本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
10.在所给的π,0,-1,$\sqrt{2}$这四个数中,最小的数是( )
| A. | π | B. | 0 | C. | -1 | D. | $\sqrt{2}$ |
7.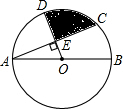 如图,⊙O的直径AB=4cm,AC是⊙O的弦,∠BAC=30°,点D在⊙O上,OD⊥AC于E,则阴影部分的面积为( )
如图,⊙O的直径AB=4cm,AC是⊙O的弦,∠BAC=30°,点D在⊙O上,OD⊥AC于E,则阴影部分的面积为( )
 如图,⊙O的直径AB=4cm,AC是⊙O的弦,∠BAC=30°,点D在⊙O上,OD⊥AC于E,则阴影部分的面积为( )
如图,⊙O的直径AB=4cm,AC是⊙O的弦,∠BAC=30°,点D在⊙O上,OD⊥AC于E,则阴影部分的面积为( )| A. | $\frac{20π-15\sqrt{3}}{30}$cm2 | B. | $\frac{24π-15\sqrt{3}}{30}$cm2 | C. | $\frac{20π-18\sqrt{3}}{30}$cm2 | D. | $\frac{20π-15\sqrt{3}}{20}$cm2 |
4.“黑洞”是恒星演化的最后阶段.根据有关理论,当一颗恒星衰老时,其中心的燃料(氢)已经被耗尽,在外壳的重压之下,核心开始坍缩,直到最后形成体积小、密度大的星体.如果这一星体的质量超过太阳质量的三倍,那么就会引发另一次大坍缩.当这种收缩使得它的半径达到施瓦氏(Schwarzschild)半径后,其引力就会变得相当强大,以至于光也不能逃脱出来,从而成为一个看不见的星体--黑洞.施瓦氏半径(单位:米)的计算公式是R=$\frac{2GM}{{c}^{2}}$,其中G=6.67×10-11牛•米2/千克2,为万有引力常数;M表示星球的质量(单位:千克);c=3×108米/秒,为光在真空中的速度.已知太阳的质量为2×1030千克,则可计算出太阳的施瓦氏半径为( )
| A. | 2.96×102米 | B. | 2.96×103米 | C. | 2.96×104米 | D. | 2.96×105米 |
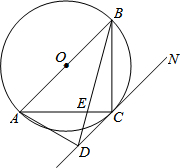 如图,AB是⊙O的直径,C是弧AB的中点,D是⊙O的切线CN上一点,BD交AC于点E,且BA=BD.
如图,AB是⊙O的直径,C是弧AB的中点,D是⊙O的切线CN上一点,BD交AC于点E,且BA=BD.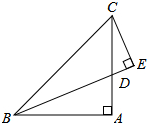 如图,已知,∠BAC=90°,AB=AC,BD是∠ABC的平分线,且CE⊥BD交BD延长线于点E.
如图,已知,∠BAC=90°,AB=AC,BD是∠ABC的平分线,且CE⊥BD交BD延长线于点E.