题目内容
13. 如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.(1)若AB=4,∠P=30°,求AP的长;
(2)若D为AP的中点,求证:直线CD是⊙O的切线.
分析 (1)首先根据切线的性质判定∠BAP=90°;然后在直角三角形ABP中利用三角函数的定义求得AP的长度;
(2)连接OC,OD、AC,构建全等三角形△OAD≌△OCD,然后利用全等三角形的对应角相等推知∠OAD=∠OCD=90°,即OC⊥CD.
解答 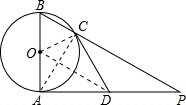 (1)解:∵AB是⊙O的直径,AP是⊙O的切线,
(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,
∴∠BAP=90°;
又∵AB=4,∠P=30°,
∴AP=$\frac{AB}{tan∠P}$=$\frac{4}{\frac{\sqrt{3}}{3}}$=4$\sqrt{3}$;
(2)证明:如图,连接OC,OD、AC.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD,
在△OAD和△OCD中,
$\left\{\begin{array}{l}{OA=OC}\\{OD=OD}\\{AD=CD}\end{array}\right.$,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD,
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,
即直线CD是⊙O的切线.
点评 本题综合考查了圆周角定理、切线的判定与性质.正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
18.64的立方根正确的是( )
| A. | ±4 | B. | 4 | C. | ±8 | D. | 8 |
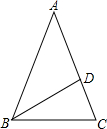 如图,在△ABC中,AB=AC,∠A=36°,点D是AC上一点,BD平分∠ABC.
如图,在△ABC中,AB=AC,∠A=36°,点D是AC上一点,BD平分∠ABC.
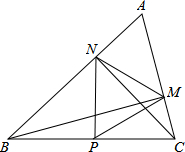 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N.P为BC边的中点,连接PM、PN,则下列结论:①PM=PN;②$\frac{AM}{AB}=\frac{AN}{AC}$;③△PMN为等边三角形;④当△ABC=45°时,BN=PC,其中正确的是①②③.(把所有正确结论的序号都选上)
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N.P为BC边的中点,连接PM、PN,则下列结论:①PM=PN;②$\frac{AM}{AB}=\frac{AN}{AC}$;③△PMN为等边三角形;④当△ABC=45°时,BN=PC,其中正确的是①②③.(把所有正确结论的序号都选上)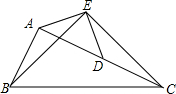 如图,在△ABC中,AC=2AB,点D是AC的中点,若BE=CE,∠ABE=∠DCE,试说明AE=DE.
如图,在△ABC中,AC=2AB,点D是AC的中点,若BE=CE,∠ABE=∠DCE,试说明AE=DE.