题目内容
2.解不等式或不等式祖,并把解集表示在数轴上.(1)1+$\frac{x}{3}$>5-$\frac{x-2}{2}$
(2)$\left\{{\begin{array}{l}{3x+2≤-4}\\{3-2x>2}\end{array}}\right.$
(3)$\left\{{\begin{array}{l}{2x+5<3(x+2)}\\{\frac{x-1}{2}-1≤\frac{x}{3}}\end{array}}\right.$.
分析 (1)去分母,移项,合并同类项,系数化成1即可.
(2)先求出两个不等式的解集,再求其公共解.
(3)先求出两个不等式的解集,再求其公共解.
解答 解:(1)1+$\frac{x}{3}$>5-$\frac{x-2}{2}$,
6+2x>30-3(x-2),
6+2x>30-3x+6,
5x>30,
x>6,
在数轴上表示不等式的解集为: .
.
(2)$\left\{\begin{array}{l}{3x+2≤-4①}\\{3-2x>2②}\end{array}\right.$
由①得:x≤-2.
由②得:x<$\frac{1}{2}$.
所以原不等式组的解集为x≤-2.
数轴表示:
(3)$\left\{\begin{array}{l}{2x+5<3(x+2)①}\\{\frac{x-1}{2}-1≤\frac{x}{3}②}\end{array}\right.$
由①得:x>-1.
由②得:x≤9.
所以原不等式组的解集为-1<x≤9.
数轴表示:
点评 本题考查了解一元一次不等式和一元一次不等式组的应用,关键是能根据不等式的解集找出不等式组的解集.

练习册系列答案
相关题目
7.函数y=$\frac{1}{\sqrt{x-1}}$中,自变量x的取值范围应是( )
| A. | x>0 | B. | x≠0 | C. | x>1 | D. | x≥1 |
14.如图图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.如果a<b,下列不等式正确的是( )
| A. | a-9>b-9 | B. | 3b<3a | C. | -2a>-2b | D. | $\frac{a}{5}$>$\frac{b}{5}$ |
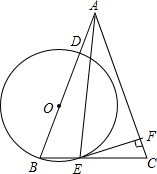 如图,在△ABC中,AB=AC,tanC=3.点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.
如图,在△ABC中,AB=AC,tanC=3.点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF. 如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C. 如图,将△AB C向右平移5个单位长度,再向下降2个单位长度,得到△A′B′C′,请画出平移后的图形,求△ABC的面积.
如图,将△AB C向右平移5个单位长度,再向下降2个单位长度,得到△A′B′C′,请画出平移后的图形,求△ABC的面积.