题目内容
9.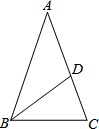 如图,在△ABC中,AB=AC,∠A=36°,点D在AC边上,连接BD,若使△ABC与△BDC相似,只需添加一个条件∠ABD=∠A(答案不唯一).
如图,在△ABC中,AB=AC,∠A=36°,点D在AC边上,连接BD,若使△ABC与△BDC相似,只需添加一个条件∠ABD=∠A(答案不唯一).
分析 由等腰三角形的性质得出∠ABC=∠C=72°,由∠ABD=∠A=36°,得出∠CBD=36°=∠A,即可证出△ABC∽△BDC.
解答 解:添加条件:∠ABD=∠A(答案不唯一);理由如下:
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵∠ABD=∠A=36°,
∴∠CBD=72°-36°=36°=∠A,
∴△ABC∽△BDC;
故答案为:∠ABD=∠A(答案不唯一).
点评 本题考查了相似三角形的判定方法、等腰三角形的性质;熟练掌握等腰三角形的性质,熟记两角相等的两个三角形相似是解决问题的关键.

练习册系列答案
相关题目
19.下列各组数据分别是三角形的三边长,其中能构成直角三角形的是( )
| A. | 2cm、4cm、5cm | B. | 1cm、1cm、$\sqrt{2}$cm | C. | 1cm、2cm、2cm | D. | $\sqrt{3}$cm、2cm、$\sqrt{5}$cm |
17.我校八年级学生去距学校15千米远的社会实践基地参加社会实践活动,一部分同学骑自行先走,过了40分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的3倍,求骑车同学的速度?
1.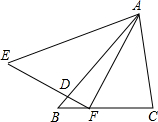 如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
①∠AFC=∠C;②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
 如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )①∠AFC=∠C;②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
| A. | 只有①③ | B. | 只有①④ | C. | 只有③④ | D. | 只有①③④ |
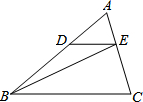 如图,在△ABC中,点D、E分别是AB、AC上的点,DE∥BC,S△ADE:S△BDE=2:3,若S△BEC=15,则S△ABC=( )
如图,在△ABC中,点D、E分别是AB、AC上的点,DE∥BC,S△ADE:S△BDE=2:3,若S△BEC=15,则S△ABC=( ) 如图为由n个相同的小正方体堆成的几何体的视图,则n=7或8或9.
如图为由n个相同的小正方体堆成的几何体的视图,则n=7或8或9.