题目内容
7.已知1辆甲型客车和1辆乙型客车共可载客75人.已知1辆甲型客车和2辆乙型客车共可载客105人.某学校计划租用两种型号客车送234名学生和6名老师集体外出活动.从安全角度考虑每辆车上至少要有1名老师,并且总费用不超过2280元.(1)求每辆甲型客车和每辆乙型客车分别可载多少人?
(2)共需租6辆客车?
(3)若每辆甲型客车和每辆乙型客车的租金分别为400元和280元,设租甲型客车x辆,总费用为W元,请你给出最节省的租车方案.
分析 (1)设每辆甲型客车可载a人,每辆乙型客车可载b人,根据“1辆甲型客车和1辆乙型客车共可载客75人,1辆甲型客车和2辆乙型客车共可载客105人”,即可得出关于a、b的二元一次方程组,解之即可得出结论;
(2)用师生人数÷甲种车型的载客量结合只有6名老师,即可得出需要租6辆客车;
(3)设租甲型客车x辆,总费用为W元,则租乙型客车(6-x)辆,根据总费用=每辆车的租金×租车数量,即可得出W关于x的函数关系式,由师生总人数结合甲、乙两种型号客车的载客量,可求出x的取值范围,再利用一次函数的性质即可解决最值问题.
解答 解:(1)设每辆甲型客车可载a人,每辆乙型客车可载b人,
根据题意得:$\left\{\begin{array}{l}{a+b=75}\\{a+2b=105}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=45}\\{b=30}\end{array}\right.$.
答:每辆甲型客车可载45人,每辆乙型客车可载30人.
(2)∵(234+6)÷45=5$\frac{1}{3}$(辆),且只有6名老师,
∴共需租6辆客车.
故答案为:6.
(3)设租甲型客车x辆,总费用为W元,则租乙型客车(6-x)辆,
根据题意得:W=400x+280(6-x)=120x+1680.
∵共有师生234+6=240(人),
∴45x+30(6-x)≥240,
解得:x≥4.
∵在W=120x+1680中,k=120>0,
∴W值随x值增大而增大,
∴当x=4时,W取最小值,最小值为2160.
答:当租甲型客车4辆、乙型客车2辆时,租车费用最少,最少费用为2160元.
点评 本题考查了一次函数的应用、二元一次方程组的应用、一次函数的性质以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)用师生人数÷甲种车型的载客量求出最少需要租车数;(3)根据总费用=每辆车的租金×租车数量,找出W关于x的函数关系式.

| A. | a(x1-x2)=k | B. | a(x2-x1)=k | C. | a(x1-x2)2=k | D. | a(x1+x2)2=k |
| A. | $\sqrt{0.5}$ | B. | $\sqrt{\frac{1}{5}}$ | C. | $\sqrt{50}$ | D. | $\sqrt{3{x}^{2}+1}$ |
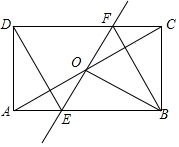 如图,点O为矩形ABCD对角线AC的中点,过点O的直线分别与AB、CD交于点E、F,连接BF、DE、BO.
如图,点O为矩形ABCD对角线AC的中点,过点O的直线分别与AB、CD交于点E、F,连接BF、DE、BO.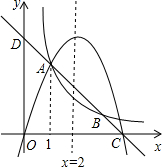 如图,在平面直角坐标系内,二次函数y=ax2+bx(a≠0)、一次函数y=ax+b(a≠0)以及反比例函数y=$\frac{k}{x}({k≠0})$的图象都经过点A,其中一次函数的图象与反比例函数的图象还交于另一点B,且一次函数与x轴、y轴分别交于点C、D.若点A的横坐标为1,该二次函数的对称轴是x=2,则下列结论:①b=-4a;②a+b>k;③8a+4b>k;④a+2b>4k.其中正确结论的个数是( )
如图,在平面直角坐标系内,二次函数y=ax2+bx(a≠0)、一次函数y=ax+b(a≠0)以及反比例函数y=$\frac{k}{x}({k≠0})$的图象都经过点A,其中一次函数的图象与反比例函数的图象还交于另一点B,且一次函数与x轴、y轴分别交于点C、D.若点A的横坐标为1,该二次函数的对称轴是x=2,则下列结论:①b=-4a;②a+b>k;③8a+4b>k;④a+2b>4k.其中正确结论的个数是( )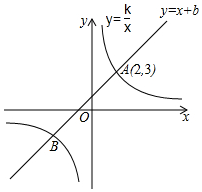 如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).
如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3). 已知数a、b、c在数轴上的位置如图所示,化简:|a+b|-|c-b|+2|c-a|的结果是3a-c.
已知数a、b、c在数轴上的位置如图所示,化简:|a+b|-|c-b|+2|c-a|的结果是3a-c.