题目内容
20.(1)如图1,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE 在∠BOC内,∠COE=2∠BOE,∠DOE=70°,求∠COE的度数.(2)如图2,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
①请你数一数,图中有9个小于平角的角;
②求出∠BOD的度数;
③请通过计算说明OE是否平分∠BOC.

分析 (1)先设∠BOE=x,根据∠BOE=$\frac{1}{2}$∠EOC,得出∠COE=2x,再根据角平分线的定义,得出∠AOD=∠DOB=70°-x,最后根据∠AOD+∠DOE+∠EOC=180°,列出方程70°-x+70°+2x=180°,求得x的值即可;
(2)①根据图形即可得出小于平角的角;②根据∠AOC=50°,OD平分∠AOC,得出∠AOD=25°,最后根据∠BOD=180°-∠AOD进行计算即可;③先根据∠AOC=50°,得出∠BOC=180°-50°=130°,再根据∠DOE=90°,求得∠BOE=∠BOD-∠DOE=155°-90°=65°,进而得出∠BOE=$\frac{1}{2}$∠BOC,即可得出结论.
解答  解:(1)如图1,设∠BOE=x,
解:(1)如图1,设∠BOE=x,
∵∠BOE=$\frac{1}{2}$∠EOC,
∴∠COE=2x,
∵OD平分∠AOB,
∴∠AOD=∠DOB=70°-x,
∵∠AOD+∠DOE+∠EOC=180°,
∴70°-x+70°+2x=180°,
解得x=40°,
∴∠EOC=80°;
(2)①由图可得,图中有9个小于平角的角,
故答案为:9;
②如图2,∵∠AOC=50°,OD平分∠AOC,
∴∠AOD=25°,
∴∠BOD=180°-∠AOD=180°-25°=155°;
③如图2,∵∠AOC=50°,
∴∠BOC=180°-50°=130°,
∵∠DOE=90°,
∴∠BOE=∠BOD-∠DOE=155°-90°=65°,
∴∠BOE=$\frac{1}{2}$∠BOC,
∴OE平分∠BOC.
点评 本题主要考查了角的计算以及角平分线的定义的运用,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.解决问题的关键是根据角的和差关系进行计算.

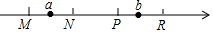 如图M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1,数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=2,则原点是N或P(填入M、N、P、R中的一个或几个).
如图M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1,数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=2,则原点是N或P(填入M、N、P、R中的一个或几个).