题目内容
12.计算:(1)32-(-$\frac{1}{2}$)-3-|1-$\sqrt{3}$|+$\sqrt{27}$-sin60°+(-2$\sqrt{5}$)0-$\frac{\sqrt{12}}{4}$
(2)[$\frac{(a+1)(a-2)}{{a}^{2}-4a+4}$-$\frac{a}{{a}^{2}-2a}$]÷$\frac{a}{a-2}$.
分析 (1)首先计算乘方,开方,去掉绝对值符号,计算0次幂,然后合并同类二次根式即可;
(2)首先对分式进行化简,然后计算分式的加减,把除法转化为乘法,然后计算乘法即可.
解答 解:(1)原式=9-(-8)-($\sqrt{3}$-1)+3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$+1-$\frac{\sqrt{3}}{2}$=9+8-$\sqrt{3}$+1+3$\sqrt{3}$+1-$\sqrt{3}$=18+$\sqrt{3}$;
(2)原式=[$\frac{(a+1)(a-2)}{(a-2)^{2}}$-$\frac{a}{a(a-2)}$]•$\frac{a-2}{a}$
=[$\frac{a+1}{a-2}$-$\frac{1}{a-2}$]•$\frac{a-2}{a}$
=$\frac{a}{a-2}$•$\frac{a-2}{a}$
=1.
点评 本题考查了实数的混合运算和分式的混合运算,正确对分式的分子、分母进行分解因式是关键.

练习册系列答案
相关题目
2.某公司准备把240吨白砂糖运往A、B两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖,相关数据见表:
(1)求大、小两种货车各用多少辆?
(2)如果安排10辆货车前往A地,其中大车有m辆,其余货车前往B地,且运往A地的白砂糖不少于130吨.
①求m的取值范围;
②请设计出总运费最少的货车调配方案,并求最少总运费.
| 载重量 | 运往A地的费用 | 运往B地的费用 | |
| 大车 | 15吨/辆 | 630元/辆 | 750元/辆 |
| 小车 | 10吨/辆 | 420元/辆 | 550元/辆 |
(2)如果安排10辆货车前往A地,其中大车有m辆,其余货车前往B地,且运往A地的白砂糖不少于130吨.
①求m的取值范围;
②请设计出总运费最少的货车调配方案,并求最少总运费.
17.若关于x的方程x2-$\sqrt{2}$x+cosα=0有两个相等实数根,则锐角α的度数为( )
| A. | 60° | B. | 45° | C. | 30° | D. | 22.5° |
2.为积极响应北京市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等.从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
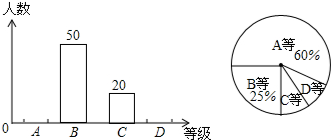

| A. | 样本容量是200 | |
| B. | 样本中C等所占百分比是10% | |
| C. | D等所在扇形的圆心角为15° | |
| D. | 估计全校学生成绩为A等大约有900人 |
 如图中的四边形均为矩形,根据图形,仅用图中出现的字母写出一个正确的等式:m(a+b+c)=ma+mb+mc.
如图中的四边形均为矩形,根据图形,仅用图中出现的字母写出一个正确的等式:m(a+b+c)=ma+mb+mc.
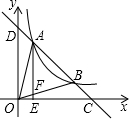 如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.