题目内容
11.若一个矩形长为m cm.宽为n cm,(m>n)(1)若这个矩形长增加2cm,宽增加2cm,则面积增加了18cm2;若这个矩形长减少1cm,宽增加1cm,则面积增加了2cm2,求$\frac{m}{n}$-$\frac{n}{m}$的值;
(2)若以m cm为边长的正方形与以n cm为边长的正方形的面积和是这个矩形面积的3倍,求$\frac{m}{n}$-$\frac{n}{m}$的值.
分析 (1)由面积上的变化关系列出关于m、n的方程组,解之得出m、n的值,再代入可得答案;
(2)根据题意得出m2+n2=3mn,变形可得m2+2mn+n2=5mn,m2-2mn+n2=mn,即(m+n)2=5mn,(m-n)2=mn,从而得出m+n=$\sqrt{5mn}$,m-n=$\sqrt{mn}$,再代入原式=$\frac{{m}^{2}-{n}^{2}}{mn}$=$\frac{(m+n)(m-n)}{mn}$即可得.
解答 解:(1)根据题意知:$\left\{\begin{array}{l}{(m+2)(n+2)-mn=18}\\{(m-1)(n+1)-mn=2}\end{array}\right.$,
整理得$\left\{\begin{array}{l}{m+n=7}\\{m-n=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=5}\\{n=2}\end{array}\right.$,
则原式=$\frac{5}{2}$-$\frac{2}{5}$=$\frac{21}{10}$;
(2)由题意知m2+n2=3mn,
则m2+2mn+n2=5mn,m2-2mn+n2=mn,
即(m+n)2=5mn,(m-n)2=mn,
∵m、n为矩形的边长,均为正数,
∴m+n=$\sqrt{5mn}$,m-n=$\sqrt{mn}$,
则原式=$\frac{{m}^{2}-{n}^{2}}{mn}$
=$\frac{(m+n)(m-n)}{mn}$
=$\frac{\sqrt{5mn}•\sqrt{mn}}{mn}$
=$\sqrt{5}$.
点评 本题主要考查分式的混合运算、二元一次方程组的应用、完全平方公式等知识点,根据面积上的相等关系列出方程组和对m2+n2=3mn利用完全平方公式变形得出m+n和m-n的值是解题的关键.

| 载重量 | 运往A地的费用 | 运往B地的费用 | |
| 大车 | 15吨/辆 | 630元/辆 | 750元/辆 |
| 小车 | 10吨/辆 | 420元/辆 | 550元/辆 |
(2)如果安排10辆货车前往A地,其中大车有m辆,其余货车前往B地,且运往A地的白砂糖不少于130吨.
①求m的取值范围;
②请设计出总运费最少的货车调配方案,并求最少总运费.
 如图,已知:AO=BO,OC=OD.求证:∠ADC=∠BCD.
如图,已知:AO=BO,OC=OD.求证:∠ADC=∠BCD. 如图,直线l1过点A(0,-5),点B(5,0),直线l2与x轴交于点C(-1,0),与y轴交于点D(0,-1),两直线l1,l2相交于点P,求△PAD的面积是4.
如图,直线l1过点A(0,-5),点B(5,0),直线l2与x轴交于点C(-1,0),与y轴交于点D(0,-1),两直线l1,l2相交于点P,求△PAD的面积是4.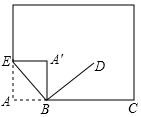 如图所示,小明将书面折过来,该角顶点A落在A′处,他以折痕BE为一边作∠DBE=90°,此时小明说BD是∠CBA′的平分线.你认为小明的说法对吗?说明你的理由.
如图所示,小明将书面折过来,该角顶点A落在A′处,他以折痕BE为一边作∠DBE=90°,此时小明说BD是∠CBA′的平分线.你认为小明的说法对吗?说明你的理由. 如图中的四边形均为矩形,根据图形,仅用图中出现的字母写出一个正确的等式:m(a+b+c)=ma+mb+mc.
如图中的四边形均为矩形,根据图形,仅用图中出现的字母写出一个正确的等式:m(a+b+c)=ma+mb+mc.