题目内容
A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD;这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有( )
A. 3种 B 4种 C 5种 D 6种
 B
【解析】试题分析:根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为:①③、②④、①②、③④四种判定方法.
B
【解析】试题分析:根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为:①③、②④、①②、③④四种判定方法.
练习册系列答案
相关题目
已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
 (1)见解析;(2)x=-2
【解析】试题分析:直接利用对称轴公式代入求出即可;根据(1)中所求,再将x=4代入方程求出a,b的值,进而解方程得出即可.
试题解析:(1)证明:∵对称轴是直线x=1=﹣,∴b=-2a ∴2a+b=0;
(2)∵ax2+bx﹣8=0的一个根为4,∴16a+4b﹣8=0,∵b=﹣2a,∴16a﹣8a﹣8=0,
解得:a=1,则b=﹣2,∴a+bx...
(1)见解析;(2)x=-2
【解析】试题分析:直接利用对称轴公式代入求出即可;根据(1)中所求,再将x=4代入方程求出a,b的值,进而解方程得出即可.
试题解析:(1)证明:∵对称轴是直线x=1=﹣,∴b=-2a ∴2a+b=0;
(2)∵ax2+bx﹣8=0的一个根为4,∴16a+4b﹣8=0,∵b=﹣2a,∴16a﹣8a﹣8=0,
解得:a=1,则b=﹣2,∴a+bx... 在□ABCD中,∠A+∠C=270°,则∠B=______,∠C=______.
 45° 135°
【解析】【解析】
∵已知平行四边形ABCD,∴∠A=∠C,∠B+∠C=180°.
又∵∠A+∠C=270°,∴2∠C=270°,∠C=135°,∴∠B=180°-∠C=180°-135°=45°.
故答案为:∠C=135°,∠B=45°.
45° 135°
【解析】【解析】
∵已知平行四边形ABCD,∴∠A=∠C,∠B+∠C=180°.
又∵∠A+∠C=270°,∴2∠C=270°,∠C=135°,∴∠B=180°-∠C=180°-135°=45°.
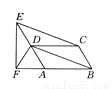
故答案为:∠C=135°,∠B=45°. 如图所示,在 ABCD中,CE∥BD,EF⊥AB交BA延长线于点F,E,D,A在一条直线上,那么有DF=
ABCD中,CE∥BD,EF⊥AB交BA延长线于点F,E,D,A在一条直线上,那么有DF=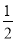 AE,请你说明理由.(提示:直角三角形中斜边中线等于斜边的一半)
AE,请你说明理由.(提示:直角三角形中斜边中线等于斜边的一半)
 答案见解析
【解析】试题分析:首先根据平行四边形的性质可得AD=BC,AD∥BC,再证明四边形EDBC是平行四边形,可得ED=CB,然后根据直角三角形斜边上的中线等于斜边的一半可得结论.
试题解析:证明:∵四边形ABCD为平行四边形,∴AD=BC,AD∥BC.∵CE∥BD,∴四边形EDBC是平行四边形,∴ED=CB,∴ED=AD.∵EF⊥AB,∴△EFA是直角三角形,∴DF=AE.
答案见解析
【解析】试题分析:首先根据平行四边形的性质可得AD=BC,AD∥BC,再证明四边形EDBC是平行四边形,可得ED=CB,然后根据直角三角形斜边上的中线等于斜边的一半可得结论.
试题解析:证明:∵四边形ABCD为平行四边形,∴AD=BC,AD∥BC.∵CE∥BD,∴四边形EDBC是平行四边形,∴ED=CB,∴ED=AD.∵EF⊥AB,∴△EFA是直角三角形,∴DF=AE. BD是□ABCD的对角线,点E,F在BD上,要使四边形AECF是平行四边形,还需添加的条件是______(只添一个你认为正确的即可).
 BE=DF等
【解析】【解析】
如图,连接AC交BD于点O.
∵四边形ABCD为平行四边形,∴AO=CO,BO=DO,∴当BE=DF时,可得OE=OF,则四边形AECF为平行四边形,∴可增加BE=DF.故答案为:BE=DF(答案不唯一).
BE=DF等
【解析】【解析】
如图,连接AC交BD于点O.
∵四边形ABCD为平行四边形,∴AO=CO,BO=DO,∴当BE=DF时,可得OE=OF,则四边形AECF为平行四边形,∴可增加BE=DF.故答案为:BE=DF(答案不唯一). A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD;这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有( )
A. 3种 B 4种 C 5种 D 6种
 B
【解析】试题分析:根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为:①③、②④、①②、③④四种判定方法.
B
【解析】试题分析:根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为:①③、②④、①②、③④四种判定方法. 已知(b+2)xb+1<-3是关于x的一元一次不等式,试求b的值,并解这个一元一次不等式.
 x<-1.5.
【解析】试题分析:先根据一元一次不等式的概念,知b+1=0,求得b,然后代入解不等式即可.
试题解析:∵(b+2)xb+1<-3是关于x的一元一次不等式,
∴b+1=1,则b=0,
∴2x<-3,
解得x<-1.5.
x<-1.5.
【解析】试题分析:先根据一元一次不等式的概念,知b+1=0,求得b,然后代入解不等式即可.
试题解析:∵(b+2)xb+1<-3是关于x的一元一次不等式,
∴b+1=1,则b=0,
∴2x<-3,
解得x<-1.5. 若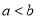 ,则下列各式中一定成立的是( )
,则下列各式中一定成立的是( )
A. 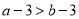 B.
B. 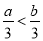 C.
C. 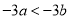 D.
D. 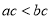
 B
【解析】因为不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变,所以A正确;不等式的两边同时乘(或除以)同一个正数,不等号的方向不变,所以B错误;因为2<3,但22<32,所以C错误;当c为负数时,ac>bc,故选A.
B
【解析】因为不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变,所以A正确;不等式的两边同时乘(或除以)同一个正数,不等号的方向不变,所以B错误;因为2<3,但22<32,所以C错误;当c为负数时,ac>bc,故选A. 计算: 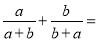 ________.
________.
 1
【解析】试题分析:原式=
=
=1.
故答案为:1.
1
【解析】试题分析:原式=
=
=1.
故答案为:1. 
