题目内容
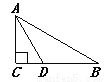
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=________.
 2
【解析】试题分析:根据角平分线性质求出∠BAD的度数,根据含30度角的直角三角形性质求出AD即可得BD.
∵∠C=90°,∠B=30°,∴∠CAB=60°,AD平分∠CAB,∴∠BAD=30°,∴BD=AD=2CD=2,
2
【解析】试题分析:根据角平分线性质求出∠BAD的度数,根据含30度角的直角三角形性质求出AD即可得BD.
∵∠C=90°,∠B=30°,∴∠CAB=60°,AD平分∠CAB,∴∠BAD=30°,∴BD=AD=2CD=2,
练习册系列答案
相关题目
在□ABCD中,∠A+∠C=270°,则∠B=______,∠C=______.
 45° 135°
【解析】【解析】
∵已知平行四边形ABCD,∴∠A=∠C,∠B+∠C=180°.
又∵∠A+∠C=270°,∴2∠C=270°,∠C=135°,∴∠B=180°-∠C=180°-135°=45°.
故答案为:∠C=135°,∠B=45°.
45° 135°
【解析】【解析】
∵已知平行四边形ABCD,∴∠A=∠C,∠B+∠C=180°.
又∵∠A+∠C=270°,∴2∠C=270°,∠C=135°,∴∠B=180°-∠C=180°-135°=45°.
故答案为:∠C=135°,∠B=45°. 已知(b+2)xb+1<-3是关于x的一元一次不等式,试求b的值,并解这个一元一次不等式.
 x<-1.5.
【解析】试题分析:先根据一元一次不等式的概念,知b+1=0,求得b,然后代入解不等式即可.
试题解析:∵(b+2)xb+1<-3是关于x的一元一次不等式,
∴b+1=1,则b=0,
∴2x<-3,
解得x<-1.5.
x<-1.5.
【解析】试题分析:先根据一元一次不等式的概念,知b+1=0,求得b,然后代入解不等式即可.
试题解析:∵(b+2)xb+1<-3是关于x的一元一次不等式,
∴b+1=1,则b=0,
∴2x<-3,
解得x<-1.5. 若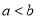 ,则下列各式中一定成立的是( )
,则下列各式中一定成立的是( )
A. 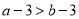 B.
B. 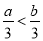 C.
C. 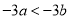 D.
D. 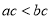
 B
【解析】因为不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变,所以A正确;不等式的两边同时乘(或除以)同一个正数,不等号的方向不变,所以B错误;因为2<3,但22<32,所以C错误;当c为负数时,ac>bc,故选A.
B
【解析】因为不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变,所以A正确;不等式的两边同时乘(或除以)同一个正数,不等号的方向不变,所以B错误;因为2<3,但22<32,所以C错误;当c为负数时,ac>bc,故选A. 已知多边形内角和与外角和的和为2160°,求多边形对角线的条数.
 54
【解析】分析:已知一个多边形的内角和与外角和的差为2160°,外角和是360度,因而内角和是1800度.n边形的内角和是(n-2) ×180°,代入就得到一个关于n的方程,就可以解得边数n,从而得到这个多边形的对角线的条数.
本题解析:
设这是n边形,则
(n-2)×180°=2160°-360°,
n-2=10,
n=12.
这个多边形的对角线的条数=12×(12...
54
【解析】分析:已知一个多边形的内角和与外角和的差为2160°,外角和是360度,因而内角和是1800度.n边形的内角和是(n-2) ×180°,代入就得到一个关于n的方程,就可以解得边数n,从而得到这个多边形的对角线的条数.
本题解析:
设这是n边形,则
(n-2)×180°=2160°-360°,
n-2=10,
n=12.
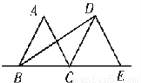
这个多边形的对角线的条数=12×(12... 如图,△ABC和△DCE都是边长为2的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为( )
A. 18 B. 3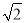 C. 12 D. 2
C. 12 D. 2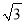
 D
【解析】过点D作DF⊥EC于点F,利用正三角形的性质得出CF=1,BF=3,再利用勾股定理求出DF==,则可得BD=.
故选:D.
D
【解析】过点D作DF⊥EC于点F,利用正三角形的性质得出CF=1,BF=3,再利用勾股定理求出DF==,则可得BD=.
故选:D. 一个直角三角形的两条直角边长分别为6 cm和8 cm,那么这个直角三角形的斜边长为( )
A. 6 cm B. 8 cm C. 10 cm D. 24 cm
 C
【解析】根据勾股定理可以得出:斜边长==10cm.
故选:C.
C
【解析】根据勾股定理可以得出:斜边长==10cm.
故选:C. 计算: 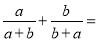 ________.
________.
 1
【解析】试题分析:原式=
=
=1.
故答案为:1.
1
【解析】试题分析:原式=
=
=1.
故答案为:1. 如图是若干张卡片,它们的背面都一样,现将它们背面朝上,从中任意摸一张卡片,摸到几号卡片的频率大?
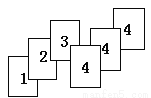
 摸到4号卡片的频率大.
【解析】试题分析: 本题考察可能性大小的应用,根据不同编号卡片的数量求出不同编号卡片被抽到的概率是解答本题的关键.
解答:因为给出的六张卡片中,1号卡片有1张,2号有1张,3号有1张,4号有3张.所以摸到1号卡片的频率为,摸到2号卡片的频率为,摸到3号卡片的频率为,摸到4号卡片的频率为.所以,摸到4号卡片的频率大.
摸到4号卡片的频率大.
【解析】试题分析: 本题考察可能性大小的应用,根据不同编号卡片的数量求出不同编号卡片被抽到的概率是解答本题的关键.
解答:因为给出的六张卡片中,1号卡片有1张,2号有1张,3号有1张,4号有3张.所以摸到1号卡片的频率为,摸到2号卡片的频率为,摸到3号卡片的频率为,摸到4号卡片的频率为.所以,摸到4号卡片的频率大. 
