Question

18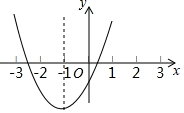．已知二次函数y=ax²+bx+c的图象如图，其对称轴是直线x=-1，给出下列结论：①b²＞4ac②abc＞0③2a+b=0④a+b+c＞0，其中正确的结论是①④（填序号）

Answer 1

分析 根据开口方向、对称轴、抛物线与y轴的交点，确定a、b、c的符号，根据对称轴和图象确定b²-4ac、2a+b、a+b+c的符号．

解答 解：①由图象得：抛物线与x轴有两个交点，
∴△＞0，即b²-4ac＞0，
b²＞4ac，
所以①正确；
②∵抛物线的开口向上，
∴a＞0，
∵-$\frac{b}{2a}$=-1＜0，
∴b＞0，
∵抛物线与y轴交于负半轴，
∴c＜0，
∴abc＜0，
所以②不正确；
③∵对称轴为直线x=-1，
∴-$\frac{b}{2a}$=-1，
∴b=2a，即2a-b=0，
所以③不正确；
④由图象得：当x=1时，y＞0，
∴a+b+c＞0，
所以④正确；
故答案为①④．

点评 本题考查的是二次函数图象与系数的关系，掌握二次函数的性质、灵活运用数形结合思想是解题的关键，解答时，要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式解决问题．