题目内容
1.某校计划从各班各抽出1名学生作为代表参加学校组织的海外游学计划,明明和华华都是本班的候选人,经过老师与同学们商量,用所学的概率知识设计摸球游戏决定谁去,设计的游戏规则如下:取M、N两个不透明的布袋,分别放入黄色和白色两种除颜色外均相同的乒乓球,其中M布袋中放置3个黄色的乒乓球和2个白色的乒乓球;N布袋中放置1个黄色的乒乓球,3个白色的乒乓球.明明从M布袋摸一个乒乓球,华华从N布袋摸一个乒乓球进行试验,若两人摸出的两个乒乓球都是黄色,则明明去;若两人摸出的两个乒乓球都是白色,则华华去;若两人摸出乒乓球颜色不一样,则放回重复以上动作,直到分出胜负为止.根据以上规则回答下列:(1)求一次性摸出一个黄色乒乓球和一个白色乒乓球的概率;
(2)判断该游戏是否公平?并说明理由.
分析 (1)画树状图列出所有等可能结果数,找到摸出一个黄色乒乓球和一个白色乒乓球的结果数,根据概率公式可得答案;
(2)结合(1)种树状图根据概率公式计算出两人获胜的概率,比较大小即可判断.
解答 解:(1)画树状图如下:
由树状图可知共有20种等可能结果,其中一次性摸出一个黄色乒乓球和一个白色乒乓球的有11种结果,
∴一次性摸出一个黄色乒乓球和一个白色乒乓球的概率为$\frac{11}{20}$;
(2)由(1)种树状图可知,明明去的概率为$\frac{3}{20}$,华华去的概率为$\frac{6}{20}$=$\frac{3}{10}$,
∵$\frac{3}{20}$$≠\frac{6}{20}$,
∴该游戏不公平.
点评 本题考查了游戏公平性问题:利用列表法或树状图法求出两个事件的概率,然后通过比较概率的大小判断游戏的公平性.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
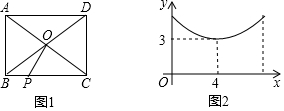
11.如图1,在矩形ABCD中,对角线AC与BD相交于点O,动点P从点B出发,在线段BC上匀速运动,到达点C时停止.设点P运动的路程为x,线段OP的长为y,如果y与x的函数图象如图2所示,则矩形ABCD的面积是( )

| A. | 20 | B. | 24 | C. | 48 | D. | 60 |
12.下列几何体中,同一个几何体的主视图与左视图不同的是( )
| A. |  圆柱 | B. |  正方体 | C. |  圆锥 | D. |  球 |
9.若代数式$\frac{1}{x-9}$有意义,则实数x的取值范围是( )
| A. | x≠0 | B. | x≥0 | C. | x≠9 | D. | x≥9 |
6.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,先从中随机摸出一个小球,再从余下的球中随机摸出一个小球,第二次摸出的小球的标号是第一次的整数倍的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
13.在亚欧商博会重点项目推介会暨签约仪式上,某公司和绵阳市政府正式签署了一个生态农牧产业园项目.该项目计划总投资21.75亿元,计划自2017年起五年内分三期建设,把21.75亿元用科学记数法表示为( )
| A. | 2.175×108元 | B. | 2.175×107元 | C. | 2.175×109元 | D. | 2.175×106元 |