题目内容
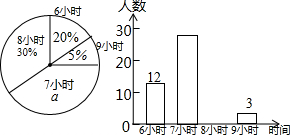
11．如图1，在矩形ABCD中，对角线AC与BD相交于点O，动点P从点B出发，在线段BC上匀速运动，到达点C时停止．设点P运动的路程为x，线段OP的长为y，如果y与x的函数图象如图2所示，则矩形ABCD的面积是（ ）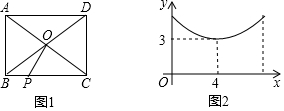
| A． | 20 | B． | 24 | C． | 48 | D． | 60 |
分析 根据点P的移动规律，当OP⊥BC时取最小值3，根据矩形的性质求得矩形的长与宽，易得该矩形的面积．
解答 解：如图2所示，当OP⊥BC时，BP=CP=4，OP=3，
所以AB=2OP=6，BC=2BP=8，
所以矩形ABCD的面积=6×8=48．
故选：C．
点评 本题考查了动点问题的函数图象，关键是根据所给函数图象和点的运动轨迹判断出BP=CP=4，OP=3．
练习册系列答案
相关题目
2．化简：$\frac{a}{{a}^{2}+2a+1}$$÷\frac{2}{（a+1）^{2}}$的结果为（ ）
| A． | $\frac{a}{a+1}$ | B． | $\frac{a}{2}$ | C． | $\frac{a+1}{a}$ | D． | 2a |
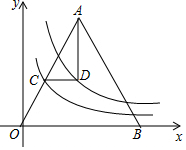如图，在△OAB中，AO=AB，S△AOB=10，函数y=$\frac{k}{x}$（x＞0）图象与OA交于点C，点D是函数y=$\frac{4}{x}$（x＞0）的图象上一点，且CD∥x轴，若∠ADC=90°，则k的值是$\frac{8}{5}$．
如图，一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是（m，-4），连接AO，AO=5，sin∠AOC=$\frac{3}{5}$．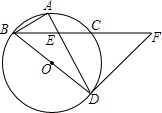
如图，BD为⊙O的直径，点A是弧BC的中点，AD交BC于E点，AE=2，ED=4．