题目内容
6.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,先从中随机摸出一个小球,再从余下的球中随机摸出一个小球,第二次摸出的小球的标号是第一次的整数倍的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
分析 画出树状图列出所有等可能结果,再根据概率公式求解可得.
解答 解:画树状图如下:
由树状图可知,共有20中等可能结果,其中第二次摸出的小球的标号是第一次的整数倍的有5种,
∴第二次摸出的小球的标号是第一次的整数倍的概率为$\frac{5}{20}$=$\frac{1}{4}$,
故选:B.
点评 此题考查了列表法或树状图法求概率.注意此题是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列各式正确的是( )
| A. | -(-2017)=2017 | B. | |-2017|=±2017 | C. | 20170=0 | D. | 2017-1=-2017 |
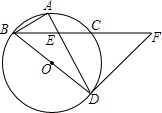 如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4.
如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4. 如图,一块呈平行四边形的菜地,被分割成3个菱形和2个平行四边形后仍是中心对称图形.若只知道原平行四边形菜地的周长,则不用测量就能知道分割后的图形的周长的图形标号为( )
如图,一块呈平行四边形的菜地,被分割成3个菱形和2个平行四边形后仍是中心对称图形.若只知道原平行四边形菜地的周长,则不用测量就能知道分割后的图形的周长的图形标号为( )