题目内容
11.已知等腰三角形的两边长分别为a、b,且a、b满足a2-6a+b2-8b+25=0,则此等腰三角形的周长为( )| A. | 9或10 | B. | 10或12 | C. | 10或11 | D. | 8或10 |
分析 利用配方法和非负数的性质求出a、b的值,根据三角形的周长公式计算即可.
解答 解:∵a2-6a+b2-8b+25=0,
∴a2-6a+9+b2-8b+16=0,
∴(a-3)2+(b-4)2=0,
解得,a=3,b=4,
则三角形的三边长为3、3、4或3、4、4,
故周长为10或11,
故选:C.
点评 本题考查的是配方法的应用和三角形的周长的计算,配方法的理论依据是公式a2±2ab+b2=(a±b)2.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
2.某校七年级学生到农科所参观,一部分同学骑自行车先走,速度为15km/h,过了40min后,其余同学乘汽车出发,速度是骑自行车同学速度的3倍,设汽车出发xh后追上骑自行车的同学,则下列方程不正确的( )
| A. | 45x=15x+$\frac{2}{3}$×15 | B. | 45x=15x+40×15 | C. | (45-15)x=$\frac{2}{3}$×15 | D. | 45x-$\frac{2}{3}$×15=15x |
9.如下列分数中,能化为有限小数的是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |
7.下列命题正确的是( )
| A. | 对角线互相平分且相等的四边形是矩形 | |
| B. | 对角线垂直的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
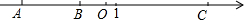 如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,CO=$\frac{5}{3}$AO.
如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,CO=$\frac{5}{3}$AO.