题目内容
6.二次函数y=x2-4x+3的图象与x轴的交点坐标是(1,0),(3,0).分析 根据抛物线与x轴的交点问题,通过解方程x2-4x+3=0即可得到抛物线与x轴的交点坐标.
解答 解:当y=0时,x2-4x+3=0,
解得:x1=1,x2=3,
所以二次函数y=x2-4x+3的图象与x轴的交点坐标是(1,0),(3,0).
故答案为(1,0),(3,0).
点评 本题考查了抛物线与x轴的交点、一元二次方程的解法;由抛物线与x轴的交点得出方程是解决问题的关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
11.已知等腰三角形的两边长分别为a、b,且a、b满足a2-6a+b2-8b+25=0,则此等腰三角形的周长为( )
| A. | 9或10 | B. | 10或12 | C. | 10或11 | D. | 8或10 |
1.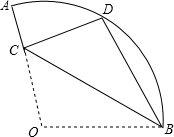 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的度数为( )
如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的度数为( )
 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的度数为( )
如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
16.下列各式中,已经化简的是( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{20}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{121}$ |