题目内容
19.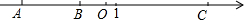 如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,CO=$\frac{5}{3}$AO.
如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,CO=$\frac{5}{3}$AO.(1)写出数轴上点A、C表示的数;
(2)若点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.
①当t为何值时,PB=4?
②若点M为线段AP的中点,点N为线段PC的中点,当点P在运动的过程,线段MN的长度发生变化吗?若不变,请求出MN的长度;若变化,请说明理由.
分析 (1)根据BO=3、AB=2BO、CO=$\frac{5}{3}$AO.结合点A、C在原点的位置关系即可得出点A、C表示的数;
(2)根据点P的运动方式可得出点P表示的数.①根据BO=3即可得出点B表示的数,结合点P表示的数已经PB=4即可得出关于t的一元一次方程,解方程即可得出结论;②根据点A、C表示的数结合点P表示的数,即可得出点M、N表示的数,由此即可得出线段MN的长度,根据MN的长度为定值即可得出结论.
解答 解:(1)∵BO=3,AB=2BO,CO=$\frac{5}{3}$AO,
∴AO=3BO=9,CO=$\frac{5}{3}$AO=15,
∵点A在原点的左侧,点C在原点的右侧,
∴点A表示的数为-9,点C表示的数为15.
(2)∵点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,
∴运动的时间为t秒时,点P表示的数为2t-9.
①∵BO=3,点B在原点的左侧,
∴点B表示的数为-3,
∴PB=|2t-9-(-3)|=|2t-6|=4,
解得:t1=1,t2=5.
答:当t的值为1秒或5秒时,PB=4.
②MN的长度不变,理由如下:
∵点A表示的数为-9,点C表示的数为15,点P表示的数为2t-9,
∴点M表示的数为t-9,点N表示的数为t+3,
∴MN=|t-9-(t+3)|=12.
∴线段MN的长度为定值12.
点评 本题考查了一元一次方程的应用以及数轴,根据线段的长度结合数轴找出各点表示的数是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
11.已知等腰三角形的两边长分别为a、b,且a、b满足a2-6a+b2-8b+25=0,则此等腰三角形的周长为( )
| A. | 9或10 | B. | 10或12 | C. | 10或11 | D. | 8或10 |
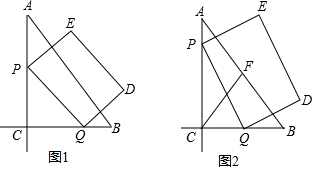
 (1)图中有哪几对互余的角?
(1)图中有哪几对互余的角? 如图,是由五个边长为2cm的小立方块搭成的几何体,一只蚂蚁想从A沿着这个几何体的表面爬到点B,它要爬行的最短路程应为2$\sqrt{5}$cm.
如图,是由五个边长为2cm的小立方块搭成的几何体,一只蚂蚁想从A沿着这个几何体的表面爬到点B,它要爬行的最短路程应为2$\sqrt{5}$cm.