题目内容
5.如图,在?ABCD中,E,F分别是AB,CD上的动点,AF与DE交于点G,CE与BF交于点H,连接GH.(1)当E,F分别运动到AB,CD的中点时,判断四边形EHFG的形状,并说明理由;
(2)试探究:
①当AE,CF满足什么条件时,一定有GH∥CD,且GH=$\frac{1}{2}$CD?
②当AE,CF满足什么条件时,四边形EHFG是平行四边形?
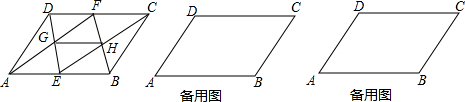
分析 (1)由在?ABCD中,点E、F分别是AB、CD的中点,易证得△AEG≌△FDG(AAS),可得EG=DG,同理可证得EH=CH,即可得GH是△ECD的中位线,继而推知四边形EHFG是平行四边形;
(2)①由在?ABCD中,点E、F分别是AB、CD的中点,易证得△AEG≌△FDG(AAS),可得EG=DG,同理可证得EH=CH,即可得GH是△ECD的中位线,继而证得结论GH∥CD,且GH=$\frac{1}{2}$CD;
②通过证明两组对边分别平行,可得四边形EHFG是平行四边形.
解答  (1)证明:如图1,∵ABCD为平行四边形,
(1)证明:如图1,∵ABCD为平行四边形,
∴DC∥AB,DC=AB,
∵E、F分别为AB、CD的中点,
∴DF=CF=$\frac{1}{2}$DC,AE=BE=$\frac{1}{2}$AB,
∴FC=AE,
∵FC∥AE,
∴四边形AECF为平行四边形,
∴AF∥EC,且AF=EC.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠GFD,
∵AE=DF,
在△AEG和△FDG中,
$\left\{\begin{array}{l}{∠GAE=∠GFD}\\{∠AGE=∠FGD}\\{AE=DF}\end{array}\right.$,
∴△AEG≌△FDG(AAS),
∴EG=DG,即点G是AF的中点.
同理:点H是EC的中点.
∴GF=EH.
∴四边形EHFG是平行四边形;
(2)当AE=CF时,一定有GH∥CD,且GH=$\frac{1}{2}$CD.
理由如下:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠GFD,
∵点E、F分别是AB、CD的中点,
∴AE=DF,
在△AEG和△FDG中,
$\left\{\begin{array}{l}{∠GAE=∠GFD}\\{∠AGE=∠FGD}\\{AE=DF}\end{array}\right.$,
∴△AEG≌△FDG(AAS),
∴EG=DG,
同理:EH=CH,
∴GH∥DC且GH=$\frac{1}{2}$DC.
②AE=CF=$\frac{1}{2}$AB时,四边形EHFG是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴AE∥CF,AB=CD,
∵AE=CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
同理可得DE∥BF,
∴四边形FGEH是平行四边形.
点评 此题考查了平行四边形的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | 由3(x-1)-5(x-2)=0,得2x=-7 | B. | 由x+1=2x-3,得x-2x=-1-3 | ||
| C. | 由$\frac{x}{2}$-$\frac{1}{3}$=1,得3x-2 | D. | 由2x=3,得x=$\frac{2}{3}$ |
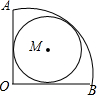 如图,已知扇形半径是1,圆心角是直角,则扇形内切圆半径是$\frac{1}{2}$.
如图,已知扇形半径是1,圆心角是直角,则扇形内切圆半径是$\frac{1}{2}$. 如图,已知∠1=∠2,∠C=∠F,请问∠A与∠D存在怎样的关系?验证你的结论.
如图,已知∠1=∠2,∠C=∠F,请问∠A与∠D存在怎样的关系?验证你的结论.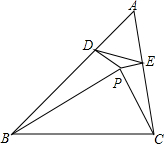 如图,在△ABC中内取一点,使∠PBA=∠PCA,作PD⊥AB于点D,PE⊥AC于点E,求证:DE的垂直平分线必过BC的中点M.
如图,在△ABC中内取一点,使∠PBA=∠PCA,作PD⊥AB于点D,PE⊥AC于点E,求证:DE的垂直平分线必过BC的中点M.