题目内容

1．解不等式组，并把解集在数轴上表示出来．
（1）$\left\{\begin{array}{l}{4x+6＞1-x}\\{3（x-1）≤x+5}\end{array}\right.$
（2）$\left\{\begin{array}{l}{2x+1＜-1}\\{3-x≥1}\end{array}\right.$．

分析 （1）首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．
（2）首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．

解答 解：（1）$\left\{\begin{array}{l}{4x+6＞1-x①}\\{3（x-1）≤x+5②}\end{array}\right.$
由①得：x＞-1，
由②得：x≤4，
所以不等式组的解集为-1＜x≤4．
在数轴上表示不等式组的解集如图所示．


（2）$\left\{\begin{array}{l}{2x+1＜-1①}\\{3-x≥1②}\end{array}\right.$
解不等式①得：x＜-1，
解不等式②得：x≤2，
所以不等式组的解集是：x＜-1；  
在数轴上表示不等式组的解集，如图所示：

点评 本题主要考查解一元一次不等式组，要遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

练习册系列答案
相关题目
20．如果三角形的一个角等于其它两个角，则这个三角形是直角三角形．
12．一元一次不等式组$\left\{\begin{array}{l}{x＜a}\\{x＜b}\end{array}\right.$的解为x＜a，则a与b的大小关系是a≤b．
9．计算：
①$\root{3}{-8}+\sqrt{{{（-3）}^2}}+|{\sqrt{3}-2}|$                      
②$\left\{{\begin{array}{l}{x+2y=9}\\{3x-2y=-1}\end{array}}\right.$．
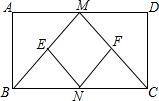16．已知：如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是线段BM、CM的中点．
（1）求证：BM=CM；
（2）判断四边形MENF是什么特殊四边形，并证明你的结论；
（3）当AD：AB=2：1时，四边形MENF是正方形（只写结论，不需证明）．
6．如图，在平面直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式$\sqrt{a-2}$+（b-3）2=0，（c-4）2≤0
（1）求a、b、c的值；
（2）如果在第二象限内有一点P（-m，$\frac{1}{2}$），请用含m的式子表示四边形ABOP的面积；
（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．
13．韦达定理：若一元二次方程ax2+bx+c=0（a≠0）的两根分别为x1、x2，则x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$，阅读下面应用韦达定理的过程：
若一元二次方程-2x2+4x+1=0的两根分别为x1、x2，求x12+x22的值．
解：该一元二次方程的△=b2-4ac=42-4×（-2）×1=24＞0
由韦达定理可得，x1+x2=-$\frac{b}{a}$=-$\frac{4}{-2}$=2，x1•x2=$\frac{c}{a}$=$\frac{1}{-2}$=-$\frac{1}{2}$
x12+x22=（x1+x2）2-2x1x2
=22-2×（-$\frac{1}{2}$）
=5
然后解答下列问题：
（1）设一元二次方程2x2+3x-1=0的两根分别为x1，x2，不解方程，求x12+x22的值；
（2）若关于x的一元二次方程（k-1）x2+（k2-1）x+（k-1）2=0的两根分别为α，β，且α2+β2=4，求k的值．
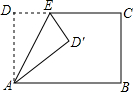10．将长方形ABCD沿AE折叠，得到如图所示的图形，若∠CED′=50°，则∠EAB的大小是65°．
11．在矩形ABCD中，AB=5，AD=12，则点A到对角线BD的距离为（　　）
A．$\frac{60}{13}$B．3C．$\frac{5}{2}$D．$\frac{13}{5}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网