题目内容
10.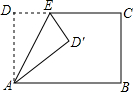 将长方形ABCD沿AE折叠,得到如图所示的图形,若∠CED′=50°,则∠EAB的大小是65°.
将长方形ABCD沿AE折叠,得到如图所示的图形,若∠CED′=50°,则∠EAB的大小是65°.
分析 首先由邻补角的定义求得∠DED′=130°,然后由翻折的性质可知:∠DEA=65°,由平行线的性质可求得∠EAB的度数.
解答 解:∵∠CED′=50°,
∴∠DED′=130°.
由翻折的性质可知:∠DEA=∠D′EA.
∴∠DEA=$\frac{1}{2}∠DED′=\frac{1}{2}×130°=65°$.
∵ABCD为矩形,
∴DC∥AB,
∴∠EAB=∠DEA=65°.
故答案为:65°.
点评 本题主要考查的是翻折变换、矩形的性质、邻补角的定义,求得∠DEA的度数是解题的关键.

练习册系列答案
相关题目
2.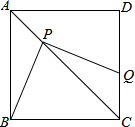 如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )
如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )
 如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )
如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )| A. | 6+4$\sqrt{2}$ | B. | 16 | C. | 12+8$\sqrt{2}$ | D. | 32 |
20.计算:$\frac{{{{(-ab)}^2}}}{{{a^2}b}}$的结果是( )
| A. | a | B. | b | C. | -b | D. | 1 |
 解不等式组,并把解集在数轴上表示出来.
解不等式组,并把解集在数轴上表示出来.
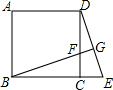 如图,在正方形ABCD中,延长BC到E,在CD上截取CF=CE,延长BF交DE于G.求证:BG⊥DE.
如图,在正方形ABCD中,延长BC到E,在CD上截取CF=CE,延长BF交DE于G.求证:BG⊥DE.