题目内容
13.韦达定理:若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1、x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,阅读下面应用韦达定理的过程:若一元二次方程-2x2+4x+1=0的两根分别为x1、x2,求x12+x22的值.
解:该一元二次方程的△=b2-4ac=42-4×(-2)×1=24>0
由韦达定理可得,x1+x2=-$\frac{b}{a}$=-$\frac{4}{-2}$=2,x1•x2=$\frac{c}{a}$=$\frac{1}{-2}$=-$\frac{1}{2}$
x12+x22=(x1+x2)2-2x1x2
=22-2×(-$\frac{1}{2}$)
=5
然后解答下列问题:
(1)设一元二次方程2x2+3x-1=0的两根分别为x1,x2,不解方程,求x12+x22的值;
(2)若关于x的一元二次方程(k-1)x2+(k2-1)x+(k-1)2=0的两根分别为α,β,且α2+β2=4,求k的值.
分析 (1)先根据根与系数的关系得到x1+x2=-$\frac{3}{2}$,x1•x2=-$\frac{1}{2}$,再利用完全平方公式变形得到x12+x22=(x1+x2)2-2x1x2,然后利用整体代入的方法计算即可;
(2)根据一元二次方程(k-1)x2+(k2-1)x+(k-1)2=0的两根分别为α,β,求出两根之积和两根之和的关于k的表达式,再将α2+β2=4变形,将表达式代入变形后的等式,解方程即可.
解答 解:(1)∵一元二次方程的△=b2-4ac=32-4×2×(-1)=17>0,
由根与系数的关系得:x1+x2=-$\frac{3}{2}$,x1•x2=-$\frac{1}{2}$,
∴x12+x22=(x1+x2)2-2x1x2=$(-\frac{3}{2})^{2}-2×(-\frac{1}{2})$=$\frac{13}{4}$;
(2)由根与系数的关系知:$α+β=\frac{{k}^{2}-1}{k-1}$=-k-1,αβ=$\frac{(k-1)^{2}}{k-1}$=k-1,
α2+β2=((α+β)2-2αβ=(k+1)2-2(k-1)=k2+3
∴k2+3=4,
∴k=±1,
∵k-1≠0
∴k≠1,
∴k=-1,
将k=-1代入原方程:-2x2+4=0,
△=32>0,
∴k=-1成立,
∴k的值为-1.
点评 本题不仅考查了一元二次方程根与系数的关系,要注意,利用根与系数的关系解题,首先要注意方程有根.

练习册系列答案
相关题目
2.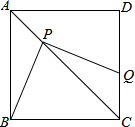 如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )
如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )
 如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )
如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )| A. | 6+4$\sqrt{2}$ | B. | 16 | C. | 12+8$\sqrt{2}$ | D. | 32 |
3.我市5月的某一周每天的最高气温(单位:℃)统计如下:29,20,27,22,24,26,27,则这组数据的中位数与众数分别是( )
| A. | 24,27 | B. | 26,27 | C. | 26,24 | D. | 20,24 |
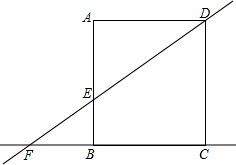 如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6.
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6. 解不等式组,并把解集在数轴上表示出来.
解不等式组,并把解集在数轴上表示出来.