题目内容
16.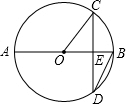 如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )| A. | $\frac{3}{2}$cm | B. | 3cm | C. | 2$\sqrt{3}$cm | D. | 9cm |
分析 先根据圆周角定理求出∠COE的度数,再由锐角三角函数的定义求出CE的长,进而可得出结论.
解答 解:∵∠COB与∠CDB是同弧所对的圆心角与圆周角,∠CDB=30°,
∴∠COB=60°.
∵弦CD⊥AB于E,
∴CE=$\frac{1}{2}$CD=OC•sin60°=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,
∴CD=3cm.
故选B.
点评 本题考查的是垂径定理与圆周角定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
6. 如图,直线a∥b,AB⊥BC,∠1=40°,则∠2的度数为( )
如图,直线a∥b,AB⊥BC,∠1=40°,则∠2的度数为( )
 如图,直线a∥b,AB⊥BC,∠1=40°,则∠2的度数为( )
如图,直线a∥b,AB⊥BC,∠1=40°,则∠2的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
11.数学活动课上,小敏、小颖分别画了△ABC和△DEF,尺寸如图.如果两个三角形的面积分别记作S△ABC、S△DEF,那么它们的大小关系是( )
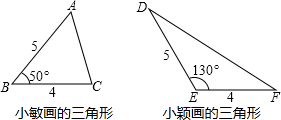

| A. | S△ABC>S△DEF | B. | S△ABC<S△DEF | C. | S△ABC=S△DEF | D. | 不能确定 |
 由几个大小相同的小正方体组成的立体图形的俯视图如左图所示,则这个立体图形应是图中的( )
由几个大小相同的小正方体组成的立体图形的俯视图如左图所示,则这个立体图形应是图中的( )



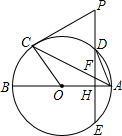 如图,已知AB,AC分别是⊙O的直径和弦,D为劣弧AC上的一点,ED为⊙O的一条弦,交AB于点H,交AC于点F,过点C画⊙O的切线交ED的延长线于点P,且PC=PF.
如图,已知AB,AC分别是⊙O的直径和弦,D为劣弧AC上的一点,ED为⊙O的一条弦,交AB于点H,交AC于点F,过点C画⊙O的切线交ED的延长线于点P,且PC=PF. 如图,AB为⊙O的弦,△ABC的两边BC、AC分别交⊙O于D、E两点,其中∠B=60°,∠EDC=70°,则∠C=50度.
如图,AB为⊙O的弦,△ABC的两边BC、AC分别交⊙O于D、E两点,其中∠B=60°,∠EDC=70°,则∠C=50度.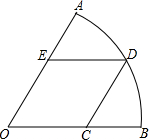 如图,扇形AOB的圆心角为60°,边长为$\sqrt{3}$的菱形OCDE的顶点C,E,D分别在OB,OA,弧AB上,则扇形AOB的面积为$\frac{3}{2}$π.(结果保留π)
如图,扇形AOB的圆心角为60°,边长为$\sqrt{3}$的菱形OCDE的顶点C,E,D分别在OB,OA,弧AB上,则扇形AOB的面积为$\frac{3}{2}$π.(结果保留π) 某校为了解九年级300名男生的体能情况,随机抽取了部分九年级男生进行“引体向上”测试,这些男生的测试成绩(单位:个)如下:
某校为了解九年级300名男生的体能情况,随机抽取了部分九年级男生进行“引体向上”测试,这些男生的测试成绩(单位:个)如下: