题目内容
3．
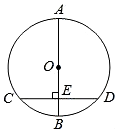如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=8，CD=6，求BE的长．
分析 连接OC，根据垂径定理得出CE=ED=$\frac{1}{2}$CD=3，然后在Rt△OEC中由勾股定理求出OE的长度，最后由BE=OB-OE，即可求出BE的长度．
解答 
解：如图，连接OC．
∵弦CD⊥AB于点E，CD=6，
∴CE=ED=$\frac{1}{2}$CD=3．
∵在Rt△OEC中，∠OEC=90°，CE=3，OC=4，
∴OE=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$，
∴BE=OB-OE=4-$\sqrt{7}$．
点评 本题主要考查了垂径定理，勾股定理等知识，关键在于熟练的运用垂径定理得出CE、ED的长度．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．已知：点A，B，C在同一条直线上，点M、N分别是AB、AC的中点，如果AB=10cm，AC=8cm，那么线段MN的长度为（ ）
| A． | 6cm | B． | 9cm | C． | 3cm或6cm | D． | 1cm或9cm |
14．
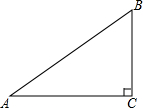如图，Rt△ABC中，∠C=90°，AC=4，BC=3，则tanA的值为（ ）
如图，Rt△ABC中，∠C=90°，AC=4，BC=3，则tanA的值为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
11．由四舍五入得到的近似数2.6万，精确到（ ）
| A． | 千位 | B． | 万位 | C． | 个位 | D． | 十分位 |
