Question

15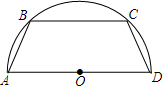．如图，四边形ABCD内接于半圆，AB=CD，BC∥AD，且AB=1，BC=2，则OA为$\frac{1+\sqrt{3}}{2}$．

Answer 1

分析 根据题意利用勾股定理表示出BE，OG的长，进而结合一元二次方程的解法得出即可．

解答 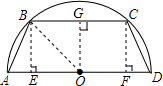解：分别过点B、点C作BE⊥AD于点E，CF⊥AD于点F，再过点O作OG⊥BC于点G，连接OB，
因为四边形ABCD是等腰梯形，AB=1，BC=2，
则BE=OG=CF，BG=GC=EO=OF=$\frac{1}{2}$EF=$\frac{1}{2}$BC=1，AB=CD=1，
设OA=OD=OB=x，
则AE=x-1，
所以BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{1-（x-1）^{2}}$=$\sqrt{2x-{x}^{2}}$，
又因为OG=$\sqrt{O{B}^{2}-B{G}^{2}}$=$\sqrt{{x}^{2}-1}$，
又因为OG=BE，
所以$\sqrt{2x-{x}^{2}}$=$\sqrt{{x}^{2}-1}$，
所以2x-x²=x²-1，
则2x²-2x-1=0，
解得：x=$\frac{1+\sqrt{3}}{2}$或$\frac{1-\sqrt{3}}{2}$（舍去），
即OA=$\frac{1+\sqrt{3}}{2}$．
故答案为：$\frac{1+\sqrt{3}}{2}$．

点评 此题主要考查了勾股定理以及垂径定理和一元二次方程的解法，表示出BE，GO的长是解题关键．