题目内容
10.(1)解下列不等式(组):$\frac{x+1}{6}$≥$\frac{2x-5}{4}$+1;(2)解不等式组$\left\{\begin{array}{l}{5x-2>3(x+1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并求其整数解.
分析 (1)先去括号,再移项,合并同类项系数化为1即可得出结论.
(2)首先解不等式组,再从不等式组的解集中找出适合条件的整数即可.
解答 解:(1)去分母得2(x+1)≥3(2x-5)+12,
去括号得2x+2≥6x-15+12,
移项得2x-6x≥-15+12-2,
合并同类项得-4x≥-5,
系数化为1得x≤$\frac{5}{4}$.
(2)$\left\{\begin{array}{l}{5x-2>3(x+1)①}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x②}\end{array}\right.$,
解不等式①得x>2.5,
解不等式②得x≤4,
∴不等式组的解集2.5<x≤4,整数解为3,4.
点评 本题考查的是解一元一次不等式(组),熟知解一元一次不等式的基本步骤和解不等式组的法则是解答此题的关键.

练习册系列答案
相关题目
5.如图表示的是用火柴棒搭成的一个个图形,第1个图形用了5根火柴,第2个图形用了8根火柴,…,照此规律,用288根火柴搭成的图形是( )


| A. | 第80个图形 | B. | 第82个图形 | C. | 第72个图形 | D. | 第95个图形 |
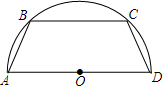 如图,四边形ABCD内接于半圆,AB=CD,BC∥AD,且AB=1,BC=2,则OA为$\frac{1+\sqrt{3}}{2}$.
如图,四边形ABCD内接于半圆,AB=CD,BC∥AD,且AB=1,BC=2,则OA为$\frac{1+\sqrt{3}}{2}$.