题目内容
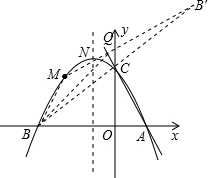
 如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(-2,
如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(-2,| 3 |
4
| ||
| 3 |
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:代数几何综合题,压轴题
分析:(1)先由抛物线的顶点坐标为N(-1,
),可设其解析式为y=a(x+1)2+
,再将M(-2,
)代入,得
=a(-2+1)2+
,解方程求出a的值即可得到抛物线的解析式;
(2)先求出抛物线y=-
x2-
x+
与x轴交点A、B,与y轴交点C的坐标,再根据勾股定理得到BC=
=2
.设P(-1,m),当△PBC为等腰三角形时分三种情况进行讨论:①CP=CB;②BP=BC;③PB=PC;
(3)先由勾股定理的逆定理得出BC⊥AC,连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,由轴对称的性质可知此时△QBM的周长最小,由B(-3,0),C(0,
),根据中点坐标公式求出B′(3,2
),再运用待定系数法求出直线MB′的解析式为y=
x+
,直线AC的解析式为y=-
x+
,然后解方程组
,即可求出Q点的坐标.
4
| ||
| 3 |
4
| ||
| 3 |
| 3 |
| 3 |
4
| ||
| 3 |
(2)先求出抛物线y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| OB2+OC2 |
| 3 |
(3)先由勾股定理的逆定理得出BC⊥AC,连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,由轴对称的性质可知此时△QBM的周长最小,由B(-3,0),C(0,
| 3 |
| 3 |
| ||
| 5 |
7
| ||
| 5 |
| 3 |
| 3 |
|
解答:解:(1)由抛物线顶点坐标为N(-1,
),可设其解析式为y=a(x+1)2+
,
将M(-2,
)代入,得
=a(-2+1)2+
,
解得a=-
,
故所求抛物线的解析式为y=-
x2-
x+
;
(2)∵y=-
x2-
x+
,
∴x=0时,y=
,
∴C(0,
).
y=0时,-
x2-
x+
=0,
解得x=1或x=-3,
∴A(1,0),B(-3,0),
∴BC=
=2
.
设P(-1,m),
当CP=CB时,有CP=
=2
,解得m=
±
;
当BP=BC时,有BP=
=2
,解得m=±2
;
当PB=PC时,
=
,解得m=0,
综上,当△PBC为等腰三角形时,点P的坐标为(-1,
+
),(-1,
-
),(-1,2
),(-1,-2
),(-1,0);
 (3)由(2)知BC=2
(3)由(2)知BC=2
,AC=2,AB=4,
所以BC2+AC2=AB2,即BC⊥AC.
连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,
∵B、B′关于直线AC对称,
∴QB=QB′,
∴QB+QM=QB′+QM=MB′,
所以此时△QBM的周长最小.
由B(-3,0),C(0,
),易得B′(3,2
).
设直线MB′的解析式为y=kx+n,
将M(-2,
),B′(3,2
)代入,
得
,解得
,
即直线MB′的解析式为y=
x+
.
同理可求得直线AC的解析式为y=-
x+
.
由
,解得
,即Q(-
,
).
所以在直线AC上存在一点Q(-
,
),使△QBM的周长最小.
4
| ||
| 3 |
4
| ||
| 3 |
将M(-2,
| 3 |
| 3 |
4
| ||
| 3 |
解得a=-
| ||
| 3 |
故所求抛物线的解析式为y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
(2)∵y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
∴x=0时,y=
| 3 |
∴C(0,
| 3 |
y=0时,-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
解得x=1或x=-3,
∴A(1,0),B(-3,0),
∴BC=
| OB2+OC2 |
| 3 |
设P(-1,m),
当CP=CB时,有CP=
1+(m-
|
| 3 |
| 3 |
| 11 |
当BP=BC时,有BP=
| (-1+3)2+m2 |
| 3 |
| 2 |
当PB=PC时,
| (-1+3)2+m2 |
1+(m-
|
综上,当△PBC为等腰三角形时,点P的坐标为(-1,
| 3 |
| 11 |
| 3 |
| 11 |
| 2 |
| 2 |
 (3)由(2)知BC=2
(3)由(2)知BC=2| 3 |
所以BC2+AC2=AB2,即BC⊥AC.
连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,
∵B、B′关于直线AC对称,
∴QB=QB′,
∴QB+QM=QB′+QM=MB′,
所以此时△QBM的周长最小.
由B(-3,0),C(0,
| 3 |
| 3 |
设直线MB′的解析式为y=kx+n,
将M(-2,
| 3 |
| 3 |
得
|
|
即直线MB′的解析式为y=
| ||
| 5 |
7
| ||
| 5 |
同理可求得直线AC的解析式为y=-
| 3 |
| 3 |
由
|
|
| 1 |
| 3 |
4
| ||
| 3 |
所以在直线AC上存在一点Q(-
| 1 |
| 3 |
4
| ||
| 3 |
点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数、一次函数的解析式,等腰三角形的性质,轴对称的性质,中点坐标公式,两函数交点坐标的求法等知识,运用数形结合、分类讨论及方程思想是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某校男子篮球队12名队员的年龄如下:16 17 17 18 15 18 16 19 18 18 19 18,这些队员年龄的众数和中位数分别是( )
| A、17,17 |
| B、17,18 |
| C、16,17 |
| D、18,18 |
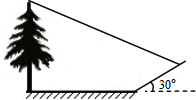 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡度为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,求树的高度.
小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡度为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,求树的高度.
 如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A(
如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A(