题目内容
4.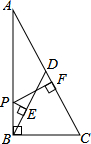 如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )
如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )| A. | $\frac{6\sqrt{5}}{5}$ | B. | $\frac{3}{2}$$\sqrt{5}$ | C. | $\frac{6}{5}$$\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{3}$ |
分析 如图作BM⊥AC于M,连接PD,利用$\frac{1}{2}$•AB•BC=$\frac{1}{2}$•AC•BM求出BM,利用S△ABC=2(S△ADP+S△BDP)即可解决问题.
解答 解:如图作BM⊥AC于M,连接PD.
∵∠ABC=90°,AD=DC,AB=6,BC=3,
∴BD=AD=DC,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=3$\sqrt{5}$,
∵$\frac{1}{2}$•AB•BC=$\frac{1}{2}$•AC•BM,
∴BM=$\frac{6\sqrt{5}}{5}$,
∴S△ABD=S△ADP+S△BDP,
∴$\frac{1}{2}$•AD•BM=$\frac{1}{2}$•AD•PF+$\frac{1}{2}$•BD•PE,
∴PE+PF=BM=$\frac{6\sqrt{5}}{5}$.
故选A.
点评 本题考查直角三角形斜边中线定理、勾股定理、三角形面积等知识,解题的关键是利用面积法求高,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列语句不是命题的是( )
| A. | 两直线平行,同位角相等 | B. | 锐角都相等 | ||
| C. | 画直线AB平行于CD | D. | 所有质数都是奇数 |
12.一个多边形的内角和是900°,则它是( )边形.
| A. | 八 | B. | 七 | C. | 六 | D. | 五 |
19.江都区三月份第一周连续七天的空气质量指数(AQI)分别为:118,96,60,82,56,69,86.则这七天空气质量变化情况最适合用哪种统计图描述( )
| A. | 扇形统计图 | B. | 条形统计图 | C. | 折线统计图 | D. | 以上都不对 |
9.估算$\sqrt{28}$的值在( )
| A. | 7和8之间 | B. | 6和7之间 | C. | 5和6之间 | D. | 4和5之间 |
16.计算下列各式的值:
(1)$\sqrt{1\frac{13}{36}}$ (2)$\root{3}{\frac{37}{64}-1}$ (3)$\root{3}{-8}$$+\sqrt{16}$.
(1)$\sqrt{1\frac{13}{36}}$ (2)$\root{3}{\frac{37}{64}-1}$ (3)$\root{3}{-8}$$+\sqrt{16}$.
13.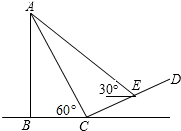 如图,小亮为测风力发电设备AB的高度,先在坡度为i=1:$\sqrt{3}$山坡CD的底部C处测得其顶端A的仰角为60°,沿山坡向上行走50米,到达点E处,测得其顶端A的仰角为30°,则该风力发电设备的高度为( )
如图,小亮为测风力发电设备AB的高度,先在坡度为i=1:$\sqrt{3}$山坡CD的底部C处测得其顶端A的仰角为60°,沿山坡向上行走50米,到达点E处,测得其顶端A的仰角为30°,则该风力发电设备的高度为( )
 如图,小亮为测风力发电设备AB的高度,先在坡度为i=1:$\sqrt{3}$山坡CD的底部C处测得其顶端A的仰角为60°,沿山坡向上行走50米,到达点E处,测得其顶端A的仰角为30°,则该风力发电设备的高度为( )
如图,小亮为测风力发电设备AB的高度,先在坡度为i=1:$\sqrt{3}$山坡CD的底部C处测得其顶端A的仰角为60°,沿山坡向上行走50米,到达点E处,测得其顶端A的仰角为30°,则该风力发电设备的高度为( )| A. | 75米 | B. | 75$\sqrt{3}$米 | C. | 25米 | D. | 25$\sqrt{3}$米 |
19.对于任意的两个实数对(a,b)和(c,d),规定以下运算:
运算“?”为:(a,b)?(c,d)=(ac+bd,bc-ad).
设p,q为任意实数,若(p,q)=(3,2),则(1,2)?(p,q)的结果等于( )
运算“?”为:(a,b)?(c,d)=(ac+bd,bc-ad).
设p,q为任意实数,若(p,q)=(3,2),则(1,2)?(p,q)的结果等于( )
| A. | (-7,4) | B. | (7,4) | C. | (2,1) | D. | (-1,-2) |
 已知一次函数y=kx+b的图象经过点(-1,-2),且与正比例函数y=$\frac{1}{2}$x的图象相交于点(2,a).
已知一次函数y=kx+b的图象经过点(-1,-2),且与正比例函数y=$\frac{1}{2}$x的图象相交于点(2,a).