题目内容
13.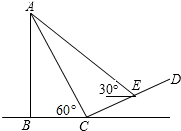 如图,小亮为测风力发电设备AB的高度,先在坡度为i=1:$\sqrt{3}$山坡CD的底部C处测得其顶端A的仰角为60°,沿山坡向上行走50米,到达点E处,测得其顶端A的仰角为30°,则该风力发电设备的高度为( )
如图,小亮为测风力发电设备AB的高度,先在坡度为i=1:$\sqrt{3}$山坡CD的底部C处测得其顶端A的仰角为60°,沿山坡向上行走50米,到达点E处,测得其顶端A的仰角为30°,则该风力发电设备的高度为( )| A. | 75米 | B. | 75$\sqrt{3}$米 | C. | 25米 | D. | 25$\sqrt{3}$米 |
分析 过点E作EF⊥AB于点F,EG⊥BC于点G,由i=1:$\sqrt{3}$得∠ECG=∠FEC=30°,继而可知∠ACE=90°、∠AEC=60°,RT△ACE中AC=CE•tan∠AEC,再根据RT△ACB中,AB=ACsin∠ACB可得.
解答 解:过点E作EF⊥AB于点F,EG⊥BC于点G,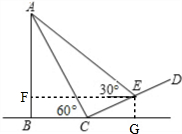
∵i=$\frac{FG}{CG}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,
∴∠ECG=∠FEC=30°,
∴∠AEC=60°,
又∵∠ACB=60°,
∴∠ACE=180°-∠ACB-∠ECG=90°,
∵CE=50m,
∴RT△ACE中,AC=CE•tan∠AEC=50×tan60°=50$\sqrt{3}$(m),
在RT△ACB中,AB=ACsin∠ACB=50$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=75(m),
故选:A.
点评 本题考查了解直角三角形的应用,要求学生借助坡角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.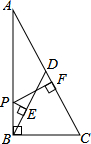 如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )
如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )
 如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )
如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )| A. | $\frac{6\sqrt{5}}{5}$ | B. | $\frac{3}{2}$$\sqrt{5}$ | C. | $\frac{6}{5}$$\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{3}$ |
18.据统计,清明小长假首日市区8个主要封闭式景区(瘦西湖、大明寺、个园、何园、茱萸湾、凤凰岛、汉陵苑、双博馆)共接待游客11.56万人次,同比增长10.48%,将数据11.56万用科学记数法表示为( )
| A. | 1.156×103 | B. | 0.1156×104 | C. | 1.156×105 | D. | 1.156×104 |
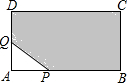 如图,长方形ABCD的边长分别为AB=12cm,AD=8cm,点P、Q都从点A出发,分别沿A-B,A-D运动,且保持AP=AQ=xcm,在这个变化过程中,图中的阴影部分的面积y(cm2)也随之变化.
如图,长方形ABCD的边长分别为AB=12cm,AD=8cm,点P、Q都从点A出发,分别沿A-B,A-D运动,且保持AP=AQ=xcm,在这个变化过程中,图中的阴影部分的面积y(cm2)也随之变化.