题目内容
19.对于任意的两个实数对(a,b)和(c,d),规定以下运算:运算“?”为:(a,b)?(c,d)=(ac+bd,bc-ad).
设p,q为任意实数,若(p,q)=(3,2),则(1,2)?(p,q)的结果等于( )
| A. | (-7,4) | B. | (7,4) | C. | (2,1) | D. | (-1,-2) |
分析 根据公式:(a,b)?(c,d)=(ac+bd,bc-ad)可求出(1,2)?(p,q)的值.
解答 解:∵(a,b)?(c,d)=(ac+bd,bc-ad),(p,q)=(3,2),
∴(1,2)?(p,q)
=(1×3+2×2,2×3-1×2)
=(7,4).
故选:B.
点评 此题主要考查了实数的运算,看懂公式的运算方法是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
4.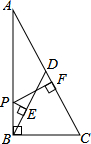 如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )
如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )
 如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )
如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )| A. | $\frac{6\sqrt{5}}{5}$ | B. | $\frac{3}{2}$$\sqrt{5}$ | C. | $\frac{6}{5}$$\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{3}$ |
14.当$\frac{a+5}{\sqrt{a-2}}$有意义时,a的取值范围是( )
| A. | a≥2 | B. | a>2 | C. | a≠2 | D. | a≠-2 |
 如图,已知AB∥CD,CE平分∠ACD,∠A:∠ACD=4:1,则∠ECD=18°.
如图,已知AB∥CD,CE平分∠ACD,∠A:∠ACD=4:1,则∠ECD=18°.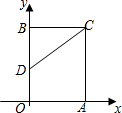 在平面直角坐标系中,矩形OABC的顶点O在标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=6,OB=8,D为边OB的中点.
在平面直角坐标系中,矩形OABC的顶点O在标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=6,OB=8,D为边OB的中点.