题目内容
9.在-$\frac{π}{3}$,$\frac{22}{7}$,$\sqrt{12}$,-$\root{3}{27}$,2$\frac{1}{2}$,6.101001000100001(1后面的0依次多1个)中,无理数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据无理数的定义以及无理数的常见形式判断并选择即可求解.
解答 解:在-$\frac{π}{3}$,$\frac{22}{7}$,$\sqrt{12}$,-$\root{3}{27}$,2$\frac{1}{2}$,6.101001000100001(1后面的0依次多1个)中,-$\frac{π}{3}$,$\sqrt{12}$,这两个数是无理数,
故选A.
点评 此题主要考查了无理数的定义.注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,$\sqrt{2}$,0.8080080008…(每两个8之间依次多1个0)等形式.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
20.菱形的边长和一条对角线长都为2,则另一条对角线长为( )
| A. | 2$\sqrt{3}$ | B. | $2\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
17.下列命题是真命题的个数是( )
①平面内不相交的两条直线叫做平行线 ②过一点有且只有一条直线与已知直线平行
③平行于同一条直线的两条直线平行 ④过一点有且只有一条直线与已知直线垂直.
①平面内不相交的两条直线叫做平行线 ②过一点有且只有一条直线与已知直线平行
③平行于同一条直线的两条直线平行 ④过一点有且只有一条直线与已知直线垂直.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.化简后能与$\sqrt{2}$是同类二次根式为( )
| A. | $\sqrt{24}$ | B. | $\sqrt{16}$ | C. | $\sqrt{\frac{1}{4}}$ | D. | $\frac{1}{\sqrt{2}}$ |
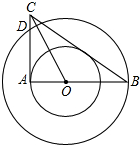 如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.