题目内容
4.化简后能与$\sqrt{2}$是同类二次根式为( )| A. | $\sqrt{24}$ | B. | $\sqrt{16}$ | C. | $\sqrt{\frac{1}{4}}$ | D. | $\frac{1}{\sqrt{2}}$ |
分析 先将各选项中的二次根式进行化简,然后求解即可.
解答 解:A、$\sqrt{24}$=2$\sqrt{6}$,与$\sqrt{2}$被开方数不同,本选项错误;
B、$\sqrt{16}$=4,与$\sqrt{2}$被开方数不同,本选项错误;
C、$\sqrt{\frac{1}{4}}$=$\frac{1}{2}$,与$\sqrt{2}$被开方数不同,本选项错误;
D、$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,与$\sqrt{2}$被开方数相同,本选项正确.
故选D.
点评 本题主要考查了同类二次根式的定义,即:化成最简二次根式后,被开方数相同,这样的二次根式叫做同类二次根式.

练习册系列答案
相关题目
14.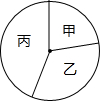 如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )
如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )
 如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )
如图,将一个圆分割成甲、乙、丙三个扇形,使它们的圆心角的度数之比为2:3:4.若圆的半径为3,则扇形丙的面积为( )| A. | $\frac{2}{3}$π | B. | $\frac{4}{9}$π | C. | 3π | D. | 4π |
 如图,在?ABCD中,AC,BD交于点O,OE⊥BD,交AD边于点E,若?ABCD的周长为20,则△ABE的周长为( )
如图,在?ABCD中,AC,BD交于点O,OE⊥BD,交AD边于点E,若?ABCD的周长为20,则△ABE的周长为( )