题目内容
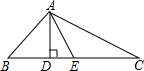 如图,△ABC中,AB=2,BC=5,AC=4.AD、AE分别为CB边上的高和中线,求DE的长.
如图,△ABC中,AB=2,BC=5,AC=4.AD、AE分别为CB边上的高和中线,求DE的长.考点:勾股定理
专题:
分析:利用中线的性质得出BE=EC的长,再利用勾股定理求出DE的长.
解答:解:∵AB=2,BC=5,AC=4,AD、AE分别为CB边上的高和中线,
∴BE=EC=2.5,
∴设DE=x,则BD=2.5-x,
故AB2-BD2=AC2-DC2,
即22-(2.5-x)2=42-(2.5+x)2,
解得:x=1.2,
故DE的长为1.2.
∴BE=EC=2.5,
∴设DE=x,则BD=2.5-x,
故AB2-BD2=AC2-DC2,
即22-(2.5-x)2=42-(2.5+x)2,
解得:x=1.2,
故DE的长为1.2.
点评:此题主要考查了勾股定理,正确得出关于DE的等式是解题关键.

练习册系列答案
相关题目
 如图,已知一个角的两边是a和b,顶点在图纸的外面,请你在图纸内画一条和这个角的平分线平行的直线,并说明你的画法是正确的.
如图,已知一个角的两边是a和b,顶点在图纸的外面,请你在图纸内画一条和这个角的平分线平行的直线,并说明你的画法是正确的.
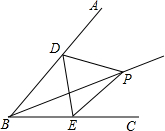 如图,已知点P是∠ABC的平分线与∠DEC的平分线的交点,求证:点P在∠ADE的平分线上.
如图,已知点P是∠ABC的平分线与∠DEC的平分线的交点,求证:点P在∠ADE的平分线上.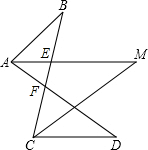 (1)如图所示,已知∠B=32°,∠D=38°,AM,CM分别平分∠BAD和∠BCD,求∠M的度数.
(1)如图所示,已知∠B=32°,∠D=38°,AM,CM分别平分∠BAD和∠BCD,求∠M的度数.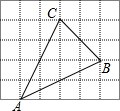 如图,网格中的每个小正方形的边长都是1,△ABC的每个顶点都在网格格点处,则sin∠CAB=
如图,网格中的每个小正方形的边长都是1,△ABC的每个顶点都在网格格点处,则sin∠CAB= 如图,△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,AB=2
如图,△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,AB=2
 如图,在△ABC中,AB=12,AC=9,BC=10,点D是AB上的一个动点,若D以2个单位长度每秒的速度,从点B出发沿边BA向点A运动,过点D作DE∥BC,交AC于点E,记x秒时DE的长度为y,请写出y关于x的函数解析式,并求自变量x的取值范围.
如图,在△ABC中,AB=12,AC=9,BC=10,点D是AB上的一个动点,若D以2个单位长度每秒的速度,从点B出发沿边BA向点A运动,过点D作DE∥BC,交AC于点E,记x秒时DE的长度为y,请写出y关于x的函数解析式,并求自变量x的取值范围.