题目内容
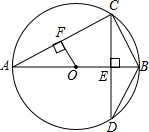 如图,AB为⊙O的直径,CD⊥AB,垂足为点E,交⊙O于点C和点D,OF⊥AC,垂足为点F.
如图,AB为⊙O的直径,CD⊥AB,垂足为点E,交⊙O于点C和点D,OF⊥AC,垂足为点F.(1)请写出三条与BC有关的正确结论;
(2)当∠D=30°,BC=1时,求AF的长.
考点:垂径定理,圆周角定理
专题:
分析:(1)直接根据垂径定理即可得出结论;
(2)先根据圆周角定理得出∠A=30°,∠ACB=90°,故可得出AC的长,再由垂径定理即可得出结论.
(2)先根据圆周角定理得出∠A=30°,∠ACB=90°,故可得出AC的长,再由垂径定理即可得出结论.
解答:解:(1)∵AB为⊙O的直径,CD⊥AB,
∴AC⊥BC,BC=BD.
∵OF⊥AC,
∴OF∥BC;
(2)∵∠D=30°,∠A=∠D,
∴∠A=30°.
∵由(1)知,∠ACB=90°,
∴AC=
=
=
.
∵OF⊥AC,
∴AF=
AC=
.
∴AC⊥BC,BC=BD.
∵OF⊥AC,
∴OF∥BC;
(2)∵∠D=30°,∠A=∠D,
∴∠A=30°.
∵由(1)知,∠ACB=90°,
∴AC=
| BC |
| tan30° |
| 1 | ||||
|
| 3 |
∵OF⊥AC,
∴AF=
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 如图,下列条件能判定a∥b的是( )
如图,下列条件能判定a∥b的是( )| A、∠1=∠2 |
| B、∠1+∠2=180° |
| C、∠2+∠3=180° |
| D、∠3=∠4 |
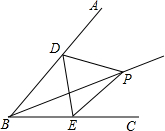 如图,已知点P是∠ABC的平分线与∠DEC的平分线的交点,求证:点P在∠ADE的平分线上.
如图,已知点P是∠ABC的平分线与∠DEC的平分线的交点,求证:点P在∠ADE的平分线上.
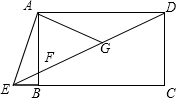 如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点.
如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点.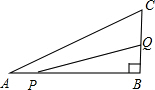 在△ABC中.∠B=90°,AB=6cm,BC=5cm,点P从点A开始,沿AB边向点B以1cm/s的速度移动,点Q从点B开始,沿BC边向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发.经过多少秒后,△PBQ的面积等于8cm2?
在△ABC中.∠B=90°,AB=6cm,BC=5cm,点P从点A开始,沿AB边向点B以1cm/s的速度移动,点Q从点B开始,沿BC边向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发.经过多少秒后,△PBQ的面积等于8cm2? 如图,在△ABC中,AB=12,AC=9,BC=10,点D是AB上的一个动点,若D以2个单位长度每秒的速度,从点B出发沿边BA向点A运动,过点D作DE∥BC,交AC于点E,记x秒时DE的长度为y,请写出y关于x的函数解析式,并求自变量x的取值范围.
如图,在△ABC中,AB=12,AC=9,BC=10,点D是AB上的一个动点,若D以2个单位长度每秒的速度,从点B出发沿边BA向点A运动,过点D作DE∥BC,交AC于点E,记x秒时DE的长度为y,请写出y关于x的函数解析式,并求自变量x的取值范围.