题目内容
13.设n为整数,且使$\frac{{n}^{2}-71}{7n+55}$为正整数,则n的值为57或-8.分析 首先设$\frac{{n}^{2}-71}{7n+55}$=k,则n2-7kn-(71+55k)=0,然后根据△=49k2+220k+284是完全平方数,求出k的值是多少;最后把求出的k的值代入n2-7kn-(71+55k)=0,求出n的值即可.
解答 解:设$\frac{{n}^{2}-71}{7n+55}$=k,
则n2-7kn-(71+55k)=0,
∵n为整数,
∴△=49k2+220k+284是完全平方数,
∵(7k+15)2<49k2+220k+284<(7k+17)2,
∴49k2+220k+284=(7k+16)2=49k2+224k+256,
解得k=7,
∴n2-49n-456=0,
∴(n+8)(n-57)=0,
解得n=57或n=-8,
即n的值为57或-8.
故答案为:57或-8.
点评 此题主要考查了分式的值的求解问题,要熟练掌握,在解答时应从已知条件和所求问题的特点出发,通过适当的变形、转化,才能发现解题的捷径.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
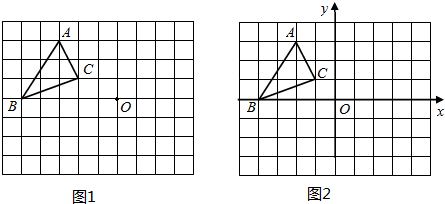
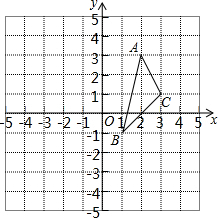 在平面直角坐标系xOy中,△ABC的位置如图所示,先把△ABC沿x轴翻折,再把所得的图形沿y轴翻折,得到△A1B1C1
在平面直角坐标系xOy中,△ABC的位置如图所示,先把△ABC沿x轴翻折,再把所得的图形沿y轴翻折,得到△A1B1C1