题目内容
4.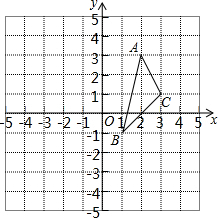 在平面直角坐标系xOy中,△ABC的位置如图所示,先把△ABC沿x轴翻折,再把所得的图形沿y轴翻折,得到△A1B1C1
在平面直角坐标系xOy中,△ABC的位置如图所示,先把△ABC沿x轴翻折,再把所得的图形沿y轴翻折,得到△A1B1C1(1)画出△A1B1C1(保留画图痕迹)并说明△ABC和△A1B1C1具有怎样的对称关系?
(2)若以坐标原点O为圆心的圆与直线AC相切,则该圆的半径长为$\frac{7\sqrt{2}}{2}$.
分析 (1)根据轴对称的性质画出图形,再由△ABC和△A1B1C1在坐标系中的位置指出其位置关系即可;
(2)连接OA,OC,设点O到直线AC的距离为h,根据勾股定理求出AC的长,再由三角形的面积即可得出h的长.
解答 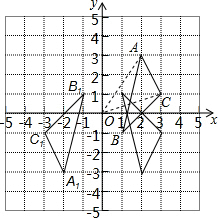 解:(1)如图所示,由图可知,△ABC和△A1B1C1关于原点对称;
解:(1)如图所示,由图可知,△ABC和△A1B1C1关于原点对称;
(2)连接OA,OC,设点O到直线AC的距离为h,
∵AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴S△OAC=$\frac{1}{2}$×$\sqrt{2}$•h=3×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×3=$\frac{7}{2}$,
∴h=$\frac{\frac{7}{2}}{\frac{\sqrt{2}}{2}}$=$\frac{7\sqrt{2}}{2}$.
∴该圆的半径长为$\frac{7\sqrt{2}}{2}$.
故答案为:$\frac{7\sqrt{2}}{2}$.
点评 此题主要考查了平移变换和轴对称变换,根据题意得出对应点位置是解题关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
9.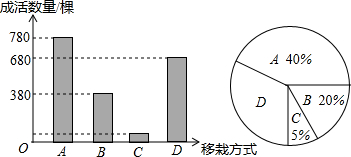 某园林部门为扩大绿化面积,进行了大量树木的移栽,他们选择A、B、C、D四种方式对2000棵树进行移栽,并分别统计四种移栽方式的成活情况,旨在提高来年移栽树木的成活率,通过计算制成下表以及两个统计图,经确认图甲有误,其它正确.
某园林部门为扩大绿化面积,进行了大量树木的移栽,他们选择A、B、C、D四种方式对2000棵树进行移栽,并分别统计四种移栽方式的成活情况,旨在提高来年移栽树木的成活率,通过计算制成下表以及两个统计图,经确认图甲有误,其它正确.
根据以上信息,解答下列问题:
(1)图2中,D种移栽方式所占的圆心角的度数为126°,D种移栽方式的树木有700棵;
(2)请指出图1中存在的错误,并说明理由;
(3)在四种移栽方式中,从所有成活的树木中随机抽取一棵,则这棵树采用B种移栽方式移栽的概率是多少?
 某园林部门为扩大绿化面积,进行了大量树木的移栽,他们选择A、B、C、D四种方式对2000棵树进行移栽,并分别统计四种移栽方式的成活情况,旨在提高来年移栽树木的成活率,通过计算制成下表以及两个统计图,经确认图甲有误,其它正确.
某园林部门为扩大绿化面积,进行了大量树木的移栽,他们选择A、B、C、D四种方式对2000棵树进行移栽,并分别统计四种移栽方式的成活情况,旨在提高来年移栽树木的成活率,通过计算制成下表以及两个统计图,经确认图甲有误,其它正确. | 移栽方式 | A | B | C | D |
| 成活率 | 97.5% | 95% | 60% | 90% |
(1)图2中,D种移栽方式所占的圆心角的度数为126°,D种移栽方式的树木有700棵;
(2)请指出图1中存在的错误,并说明理由;
(3)在四种移栽方式中,从所有成活的树木中随机抽取一棵,则这棵树采用B种移栽方式移栽的概率是多少?
14.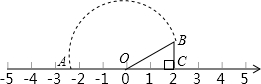 如图所示,点C的表示的数为2,BC=1,以O为圆心,OB为半径画弧,交数轴于点A,则点A表示的数是( )
如图所示,点C的表示的数为2,BC=1,以O为圆心,OB为半径画弧,交数轴于点A,则点A表示的数是( )
 如图所示,点C的表示的数为2,BC=1,以O为圆心,OB为半径画弧,交数轴于点A,则点A表示的数是( )
如图所示,点C的表示的数为2,BC=1,以O为圆心,OB为半径画弧,交数轴于点A,则点A表示的数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | -$\sqrt{3}$ | D. | -$\sqrt{5}$ |

 如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,$\frac{OD}{BD}$=$\frac{1}{2}$.
如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,$\frac{OD}{BD}$=$\frac{1}{2}$.