题目内容
8.不解方程,判别下列方程根的情况.(1)x2+2x-3=0;
(2)5x2=-2(x-10);
(3)8x2+(m+1)x+m-7=0.
分析 把各式化成一元二次方程的一般式,求出根的判别式△=b2-4ac,然后判断是否有实数根.
解答 解:(1)x2+2x-3=0;
△=b2-4ac=4+12=16>0,
故方程有两不相等的实数根,
(2)5x2=-2(x-10);
原方程可化为5x2+2x-20=0,
△=b2-4ac=4+4×5×20=404>0,
故方程有两不相等的实数根,
(3)8x2+(m+1)x+m-7=0,
△=(m+1)2-4×8(m-7)=(m-15)2≥0故方程有实数根.
点评 本题主要考查根的判别式的知识点,当△=b2-4ac>0,方程有两不等的实数根,当△=b2-4ac=0,方程有两相等的实数根,△=b2-4ac<0,方程没有实数根.

练习册系列答案
相关题目
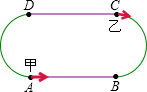 已知甲、乙两人在一个200米的环形跑道上练习跑步,现在把跑道分为相等的4段,即两条直跑道和两条弯道的长度相等.甲平均每秒跑4米,乙平均每秒跑6米.若甲、乙两人分别从A、C两处同时出发(如图),则他们第100次相遇时在跑道( DA )上(填“AB”或“BC”或“DA”或“CD”)
已知甲、乙两人在一个200米的环形跑道上练习跑步,现在把跑道分为相等的4段,即两条直跑道和两条弯道的长度相等.甲平均每秒跑4米,乙平均每秒跑6米.若甲、乙两人分别从A、C两处同时出发(如图),则他们第100次相遇时在跑道( DA )上(填“AB”或“BC”或“DA”或“CD”)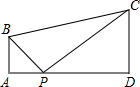 如图,四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=7,AB=2,DC=3,P为AD上一点,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,那么这样的点P有几个?为什么?
如图,四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=7,AB=2,DC=3,P为AD上一点,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,那么这样的点P有几个?为什么?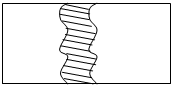 如图所示,在一块长为a米,宽为b米的长方形地上,有一条弯曲的柏油马路,马路任何地方的水平宽度都是2米,其他部分都是草地.求草地的面积.
如图所示,在一块长为a米,宽为b米的长方形地上,有一条弯曲的柏油马路,马路任何地方的水平宽度都是2米,其他部分都是草地.求草地的面积.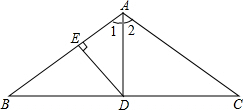 如图,在△ABC中,AB=AC,∠C=30°,D是BC边上中点,DE⊥AB于点E,BC=12,求:
如图,在△ABC中,AB=AC,∠C=30°,D是BC边上中点,DE⊥AB于点E,BC=12,求: 如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,$\frac{OD}{BD}$=$\frac{1}{2}$.
如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,$\frac{OD}{BD}$=$\frac{1}{2}$.