题目内容
7.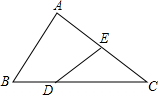 如图,在△ABC中,点D在边BC上,且DC=2BD,点E是边AC的中点,设$\overrightarrow{BC}=\vec a,\overrightarrow{AC}=\vec b$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$;(用不$\vec a、\vec b$的线性组合表示)
如图,在△ABC中,点D在边BC上,且DC=2BD,点E是边AC的中点,设$\overrightarrow{BC}=\vec a,\overrightarrow{AC}=\vec b$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$;(用不$\vec a、\vec b$的线性组合表示)
分析 由在△ABC中,点D在边BC上,且DC=2BD,点E是边AC的中点,设$\overrightarrow{BC}=\vec a,\overrightarrow{AC}=\vec b$,可表示出$\overrightarrow{DC}$与$\overrightarrow{EC}$,然后利用三角形法则求解即可求得答案.
解答 解:∵DC=2BD,点E是边AC的中点,设$\overrightarrow{BC}=\vec a,\overrightarrow{AC}=\vec b$,
∴$\overrightarrow{DC}$=$\frac{2}{3}$$\overrightarrow{BC}$=$\frac{2}{3}$$\overrightarrow{a}$,$\overrightarrow{EC}$=$\frac{1}{2}$$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{b}$,
∴$\overrightarrow{DE}$=$\overrightarrow{DC}$-$\overrightarrow{EC}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$.
故答案为:$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.不等式组$\left\{\begin{array}{l}{x-3(x-2)≤8}\\{5-\frac{1}{2}x>2x}\end{array}\right.$的最大整数解是( )
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
2.下列一元二次方程中,有两个相等实数根的是( )
| A. | x2-8=0 | B. | 2x2-4x+3=0 | C. | 9x2-6x+1=0 | D. | 5x+2=3x2 |
19.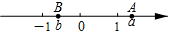 如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
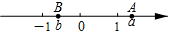 如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )| A. | ab>0 | B. | a+b>0 | C. | (a-1)(b-1)>0 | D. | (a+1)(b-1)>0 |
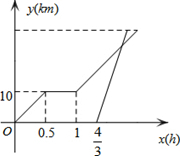 周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后,按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车速度是小明的3倍.
周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后,按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车速度是小明的3倍.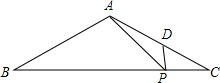 已知:如图,在△ABC中,AB=AC=13,BC=24,点P、D分别在边BC、AC上,AP2=AD•AB,求∠APD的正弦值.
已知:如图,在△ABC中,AB=AC=13,BC=24,点P、D分别在边BC、AC上,AP2=AD•AB,求∠APD的正弦值.