题目内容
17.解不等式组$\left\{\begin{array}{l}{x+5≥3①}\\{\frac{x-3}{2}<-1②}\end{array}\right.$请结合题意填空,完成本题的解答
(1)解不等式①,得x≥-2
(2)解不等式②,得x<1
(3)把不等式①和②的解集在数轴上表示出来
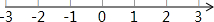
(4)原不等式组的解集为-2≤x<1.
分析 (1)通过移项可得到x的范围;
(2)去分母,再移项可得到x的范围;
(3)利用数轴表示解集;
(4)利用大小小大中间找;
解答 解:(1)解不等式①,得x≥-2,
(2)解不等式②,得x<1,
(3)把不等式①和②的解集在数轴上表示为:
(4)原不等式组的解集为-2≤x<1.
故答案为x≥-2,x<1,-2≤x<1.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
8.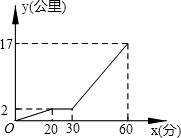 星期天下午,小强和小明相约在某公交车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
星期天下午,小强和小明相约在某公交车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
 星期天下午,小强和小明相约在某公交车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
星期天下午,小强和小明相约在某公交车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )| A. | 小强从家到公共汽车站步行了2千米 | |
| B. | 小强在公共汽车站等小明用了10分钟 | |
| C. | 公交车的平均速度是34千米/小时 | |
| D. | 小强乘公交车用了30分钟 |
2.函数y=$\frac{\sqrt{x+1}}{x+3}$中自变量x的取值范围是( )
| A. | x≥-1 | B. | x≠-3 | C. | x≥-1且x≠-3 | D. | x<-1 |
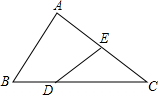 如图,在△ABC中,点D在边BC上,且DC=2BD,点E是边AC的中点,设$\overrightarrow{BC}=\vec a,\overrightarrow{AC}=\vec b$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$;(用不$\vec a、\vec b$的线性组合表示)
如图,在△ABC中,点D在边BC上,且DC=2BD,点E是边AC的中点,设$\overrightarrow{BC}=\vec a,\overrightarrow{AC}=\vec b$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$;(用不$\vec a、\vec b$的线性组合表示) 已知气温的华氏度数y是摄氏度数x的一次函数,如图所示是一个家用温度表的表盘,其左边为摄氏温度的刻度和度数(单位:℃),右边为华氏温度的刻度和度数(单位:℉),观察发现表示-40℃与-40℉的刻度线恰好对齐(左一条水平线上),而表示0℃与32℉的刻度线恰好对齐.
已知气温的华氏度数y是摄氏度数x的一次函数,如图所示是一个家用温度表的表盘,其左边为摄氏温度的刻度和度数(单位:℃),右边为华氏温度的刻度和度数(单位:℉),观察发现表示-40℃与-40℉的刻度线恰好对齐(左一条水平线上),而表示0℃与32℉的刻度线恰好对齐.