题目内容
12.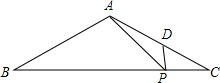 已知:如图,在△ABC中,AB=AC=13,BC=24,点P、D分别在边BC、AC上,AP2=AD•AB,求∠APD的正弦值.
已知:如图,在△ABC中,AB=AC=13,BC=24,点P、D分别在边BC、AC上,AP2=AD•AB,求∠APD的正弦值.
分析 由AP2=AD•AB,AB=AC,可证得△ADP∽△APC,由相似三角形的性质得到∠APD=∠ACB=∠ABC,作AE⊥BC于E,根据等腰三角形的性质可求得AE,由三角函数的定义可得结论,
解答 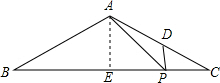 解:∵AP2=AD•AB,AB=AC,
解:∵AP2=AD•AB,AB=AC,
∴AP2=AD•AC,
$\frac{AP}{AC}=\frac{AD}{AP}$,
∵∠PAD=∠CAP,
∴△ADP∽△APC,
∴∠APD=∠ACB=∠ABC,
作AE⊥BC于E,
∵AB=AC,
∴BE=CE=$\frac{1}{2}$×24=12,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=5
∴sin∠APD=sin∠ABC=$\frac{5}{13}$,
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
3.下列运算中,结果是a5的是( )
| A. | a10÷a2 | B. | a2•a3 | C. | (a2)3 | D. | (-a)5 |
20.函数y=$\frac{1}{|x|}$的图象是( )
| A. |  | B. |  | C. |  | D. |  |
17.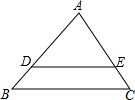 如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )
如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )
 如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )
如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )| A. | 6 | B. | 4.5 | C. | 2 | D. | 1.5 |
2.函数y=$\frac{\sqrt{x+1}}{x+3}$中自变量x的取值范围是( )
| A. | x≥-1 | B. | x≠-3 | C. | x≥-1且x≠-3 | D. | x<-1 |
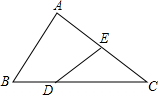 如图,在△ABC中,点D在边BC上,且DC=2BD,点E是边AC的中点,设$\overrightarrow{BC}=\vec a,\overrightarrow{AC}=\vec b$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$;(用不$\vec a、\vec b$的线性组合表示)
如图,在△ABC中,点D在边BC上,且DC=2BD,点E是边AC的中点,设$\overrightarrow{BC}=\vec a,\overrightarrow{AC}=\vec b$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$;(用不$\vec a、\vec b$的线性组合表示)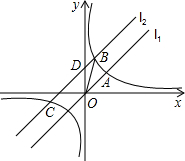 如图,直线l1:y=x与反比例函数$y=\frac{k}{x}$的图象c相交于点A(2,a),将直线l1向上平移3个单位长度得到l2,直线l2与c相交于B,C两点,(点B在第一象限),交y轴于点D.
如图,直线l1:y=x与反比例函数$y=\frac{k}{x}$的图象c相交于点A(2,a),将直线l1向上平移3个单位长度得到l2,直线l2与c相交于B,C两点,(点B在第一象限),交y轴于点D.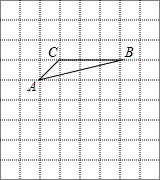 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.