题目内容
17.△ADE中,AE=AD且∠EAD=90°.
(1)如图1,若EC、DB分别平分∠AED、∠ADE,交AD、AE于点C、B,连接BC,请你判断AB、AC是否相等,并说明理由;
(2)△ADE的位置保持不变,将(1)中的△ABC绕点A逆时针旋转至图(2)的位置,线段CD与BE相交于点O,请你判断线段BE与CD的位置关系及数量关系,并说明理由.
分析 (1)由已知得∠AEC=∠ADB,AE=AD,∠A=∠A,利用“ASA”证明△AEC≌△ADB即可得出结论;
(2)由旋转的性质可证△AEB≌△ADC,从而可得BE=CD,再利用角的相等关系,互余关系证明BE⊥CD.
解答 解:(1)AB=AC.理由如下:
∵EC、DB分别平分∠AED、∠ADE,
∴∠AEC=$\frac{1}{2}$∠AED,∠ADB=$\frac{1}{2}$∠ADE,
∵∠AED=∠ADE,
∴∠AEC=∠ADB,
∵在△AEC和△ADB中,∠AEC=∠ADB,AE=AD,∠A=∠A,
∴△AEC≌△ADB,
∴AB=AC;
(2)BE=CD且BE⊥CD.理由如下:
∵∠EAD=∠BAC,
∴∠EAB=∠DAC,
∵在△AEB和△ADC中,AB=AC,∠EAB=∠DAC,AE=AD,
∴△AEB≌△ADC(SAS),
∴EB=CD,
∴∠AEB=∠ADC,
∵∠AEB+∠DEB+∠ADE=90°,
∴∠ADC+∠DEB+∠ADE=90°,
∵∠ADC+∠DEB+∠ADE+∠DOE=180°,
∴∠DOE=90°,
∴BE⊥CD.
点评 本题考查了旋转的性质以及全等三角形的判定和性质;解决问题的关键是运用角的相等关系,线段的相等关系将问题进行转化.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
9.已知:$\sqrt{10n}$是整数,则满足条件的最小正整数n为( )
| A. | 4 | B. | 8 | C. | 9 | D. | 10 |
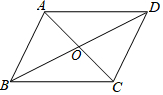 如果平行四边形ABCD的对角线AC、BD相交于O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示向量$\overrightarrow{OC}$.
如果平行四边形ABCD的对角线AC、BD相交于O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示向量$\overrightarrow{OC}$.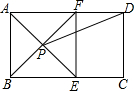 如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.